题目内容
2.先化简再求值:$\frac{{x}^{2}-{y}^{2}}{xy-{x}^{2}}$÷(x+$\frac{2xy+{y}^{2}}{x}$)($\frac{1}{x}$+$\frac{1}{y}$),其中x=2,y=-$\frac{1}{2}$.分析 首先化简$\frac{{x}^{2}-{y}^{2}}{xy-{x}^{2}}$÷(x+$\frac{2xy+{y}^{2}}{x}$)($\frac{1}{x}$+$\frac{1}{y}$),然后把x=2,y=-$\frac{1}{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{{x}^{2}-{y}^{2}}{xy-{x}^{2}}$÷(x+$\frac{2xy+{y}^{2}}{x}$)($\frac{1}{x}$+$\frac{1}{y}$)
=-$\frac{x+y}{x}$÷$\frac{{(x+y)}^{2}}{x}$×$\frac{x+y}{xy}$
=-$\frac{1}{x+y}$×$\frac{x+y}{xy}$
=-$\frac{1}{xy}$
当x=2,y=-$\frac{1}{2}$时,
原式=-$\frac{1}{2×(-\frac{1}{2})}$=1.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
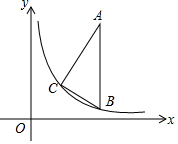 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.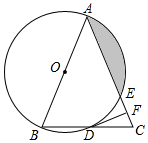 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.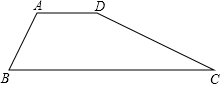 如图,已知四边形ABCD中,AD∥BC,AB=AD.
如图,已知四边形ABCD中,AD∥BC,AB=AD.