Question

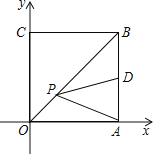
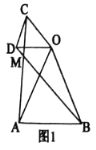
【题目】为庆祝新中国成立70周年，国庆期间，北京举办“普天同庆共筑中国梦”的游园活动，为此，某公园在中央广场处建了一个人工喷泉，如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2m，喷出水流的运动路线是抛物线．如果水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3.6m，求水流的落地点C到水枪底部B的距离．

Answer 1

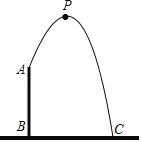
【答案】水流的落地点C到水枪底部B的距离为2.5m．

【解析】

如图，建立以所在直线为轴、所在直线为轴的直角坐标系，根据顶点设其解析式为，把代入求得的值，据此可得其函数解析式；求得时的值可得答案．

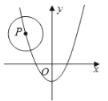
如图，以BC所在直线为x轴、AB所在直线为y轴建立直角坐标系，

由题意知，抛物线的顶点P的坐标为(1,3.6)、点A(0,2)，

设抛物线的解析式为y＝a（x﹣1）2+3.6，

将点A(0,2)代入，得：a+3.6＝2，

解得：a＝﹣1.6，

则抛物线的解析式为y＝﹣1.6（x﹣1）2+3.6，

当y＝0时，有﹣1.6（x﹣1）2+3.6＝0，

解得：x＝﹣0.5（舍）或x＝2.5，

∴BC＝2.5，

答：水流的落地点C到水枪底部B的距离为2.5m．