题目内容
如图，AC是⊙O的直径，CB与⊙O相切于点C，AB交⊙O于点D．已知∠B=51°，则∠DOC等于 度．
【答案】分析：根据切线的性质定理及三角形内角和可求得∠A的度数，再根据一条弧所对的圆周角等于它所对的圆心角的一半即可求解．
解答：解：∵CB与⊙O相切于点C
∴AC⊥BC
∵∠B=51°
∴∠A=90°-∠B=39°
∴∠COD=2∠A=78°．
点评：综合运用了切线的性质定理以及圆周角定理．
解答：解：∵CB与⊙O相切于点C
∴AC⊥BC
∵∠B=51°
∴∠A=90°-∠B=39°
∴∠COD=2∠A=78°．
点评：综合运用了切线的性质定理以及圆周角定理．
练习册系列答案
相关题目
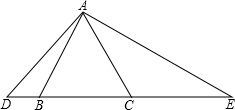如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
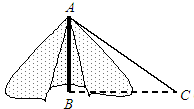在“汶川”地震后人们积极开展自救．如图，这是小明家搭建的简易帐篷，小明准备从帐篷竖直的支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷．若地面固定点C到帐篷支撑竿底部B的距离是4米，∠ACB=30°，求支撑竿AB的长和绳子AC的长．（结果保留根号）．
某市的跨江斜拉大桥建成通车，如图，BC是水平桥面，AD是竖直桥墩，按工程设计的要求，斜拉的钢线AB、AC应相等，请你用学过的知识来检验AB、AC的长度是相等的，写出你的检验方法步骤，并简要说明理由．（检验工具为刻度尺、测角仪；检验时，人只能站在桥面上）
