Question

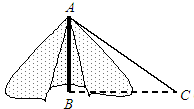在“汶川”地震后人们积极开展自救．如图，这是小明家搭建的简易帐篷，小明准备从帐篷竖直的支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷．若地面固定点C到帐篷支撑竿底部B的距离是4米，∠ACB=30°，求支撑竿AB的长和绳子AC的长．（结果保留根号）．

Answer 1

分析：在直角三角形中ABC中，利用角C的正切，求出AB，再由勾股定理求得AC．

解答：解：由题意：∵AB⊥BC，BC=4米，∠C=30°．
∴AB=BC•tan30°=4×

3

3

=

4

3

3

(米)．
AC=2AB=

8

3

3

(米)．
答：支撑竿AB的长为

4 3

3

米，绳子AC的长为

8 3

3

米．

点评：本题考查了解直角三角形的应用，一个角的正切值等于对边比邻边．