题目内容
2．在△ABC中AB=AC，AC上的中线BD把三角形的周长分为12和18的两个部分，求三角形的三边长．分析 首先根据题意画出图形，然后根据题意列出方程，注意分别从AB+AD=18与AB+AD=12去分析求解即可求得答案．
解答 
解：根据题意画出图形，如图，
设等腰三角形的腰长AB=AC=2x，BC=y，
∵BD是腰上的中线，
∴AD=DC=x，
若AB+AD的长为12，则2x+x=12，解得x=4，
则x+y=18，即4+y=18，解得y=14；
∴等腰三角形的腰长为8，底边长为14．
若AB+AD的长为18，则2x+x=18，解得x=6，
则x+y=12，即6+y=12，解得y=6；
∴等腰三角形的腰长为12，底边长为6．
综上三角形的三边长分别为：8，8，14或12，12，6．
点评 此题考查了等腰三角形的性质．注意根据题意画出图形，利用分类讨论思想求解是关键．
练习册系列答案
相关题目
12．下列运用等式的性质变形错误的是（ ）
| A． | 若a=b，则a+1=b+1 | B． | 若-3x=-3y，则x=-y | ||
| C． | 若n-2=m-2，则m-n=0 | D． | 若$\frac{a}{2}$=$\frac{b}{2}$，则a=b |
如图，Rt△ABC中，∠A=30°，AB=12cm，则BC=6cm．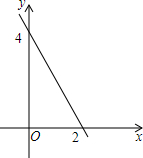
一次函数y=kx+b的图象如图所示，根据图象回答：