Question

19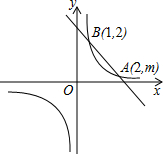．直线y₁=k₁x+b与双曲线y₂=$\frac{{k}_{2}}{x}$相交于A（2，m），B（1，2）两点．
（1）求直线和双曲线的解析式；
（2）直接写出y₁＞y₂时自变量x的取值范围．

Answer 1

分析 （1）先把B点坐标代入y=$\frac{{k}_{2}}{x}$求出k₂=2，得到双曲线的解析式为y=$\frac{2}{X}$，再把A（2，m）代入y=$\frac{2}{x}$确定a点坐标，然后利用待定系数法确定一次函数的解析式；
（2）观察函数图象得到结论．

解答 解：（1）∵直线y₁=k₁x+b与双曲线y₂=$\frac{{k}_{2}}{x}$相交于A（2，m），B（1，2）两点．
∴k₂=2，m=1，
∴A（2，1），双曲线的解析式为：y=$\frac{2}{x}$，
∴$\left\{\begin{array}{l}{1=2k+b}\\{2=k+b}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$，
∴直线的解析式为y=-x+3；
（2）由图象知y₁＞y₂时自变量x的取值范围是：1＜x＜2或x＜0．

点评 本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式以及观察函数图象的能力．