题目内容
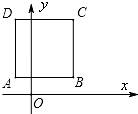
如图,在平面直角坐标系中,直线 y=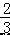 x﹣
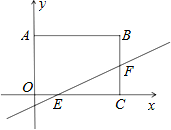
x﹣ 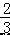 与矩形 ABCO 的边 OC、BC 分别交于点 E、F,已 知 OA=3,OC=4,则△CEF 的面积是( )
与矩形 ABCO 的边 OC、BC 分别交于点 E、F,已 知 OA=3,OC=4,则△CEF 的面积是( )
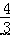 A.6 B.3 C.12 D.
A.6 B.3 C.12 D.
B考点】一次函数综合题.
【专题】综合题.
【分析】根据直线解析式分别求出点 E、F 的坐标,然后利用三角形的面积公式求解即可.
【解答】解:当 y=0 时,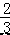 x﹣
x﹣ 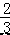 =0, 解得 x=1,
=0, 解得 x=1,
∴点 E 的坐标是(1,0),即 OE=1,
∵OC=4,
∴EC=OC﹣OE=4﹣1=3,
∴点 F 的横坐标是 4,
∴y= 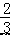 ×4﹣
×4﹣ 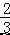 =2,即 CF=2,
=2,即 CF=2,
∴△CEF 的面积=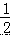 ×CE×CF=
×CE×CF= 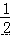 ×3×2=3.
×3×2=3.
故选 B.
【点评】本题是对一次函数的综合考查,根据直线的解析式求出点 E、F 的坐标是解题的关键,同时 也考查了矩形的性质,难度不大.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
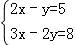 解方程组 .
解方程组 .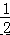 BC,连接 DE,CF.
BC,连接 DE,CF.
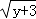 =0.
=0.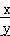 )2015 的值?
)2015 的值?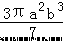 与 是同类项.
与 是同类项.