题目内容
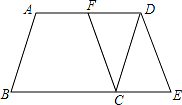
如图,在▱ABCD 中,F 是 AD 的中点,延长 BC 到点 E,使 CE=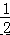 BC,连接 DE,CF.
BC,连接 DE,CF.
(1)求证:四边形 CEDF 是平行四边形; 若 AB=4,AD=6,∠B=60°,求 DE 的长.
【考点】平行四边形的判定与性质;含 30 度角的直角三角形;勾股定理.
【分析】(1)由“平行四边形的对边平行且相等”的性质推知 AD∥BC,且 AD=BC;然后根据中点的 定义、结合已知条件推知四边形 CEDF 的对边平行且相等(DF=CE,且 DF∥CE),即四边形 CEDF 是平行四边形;
如图,过点 D 作 DH⊥BE 于点 H,构造含 30 度角的直角△DCH 和直角△DHE.通过解直角△DCH 和在直角△DHE 中运用勾股定理来求线段 ED 的长度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
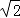
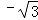 .
.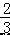 x﹣
x﹣ 
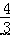 A.6 B.3 C.12 D.
A.6 B.3 C.12 D.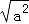 =﹣a,则实数 a 一定不在数轴原点右侧
=﹣a,则实数 a 一定不在数轴原点右侧