题目内容
某商场代销甲、乙两种商品,其中甲种商品的进价为 120 元/件,售件为 130 元/件,乙种商品的
进价为 100 元/件,售件为 150 元/件.
(1)若商场用 36000 元购进这两种商品,销售完后可获得利润 6000 元,则该商场购进甲、乙两种 商品各多少件?
若商场要购进这两种商品共 200 件,设购进甲种商品 x 件,销售后获得的利润为 W 元,试写出利润 W(元)与 x(件)函数关系式(不要求写出自变量 x 的取值范围);并指出购进甲种商品件数 x 逐 渐增加时,利润 W 是增加还是减少?
【考点】一次函数的应用;二元一次方程组的应用.
【分析】(1)设购进甲种商品 x 件,乙种商品 y 件,根据销售问题的数量关系建立方程组求出其解 即可;
(1)由购进甲种商品 x 件,则购进乙种商品件,由利润等于售价﹣进价建立函数关系式就可以得出 结论.
【解答】解:(1)设购进甲种商品 x 件,乙种商品 y 件,由题意,得
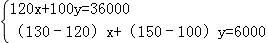 ,
,
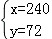 解得:
解得:
答:该商场购进甲种商品 240 件,乙种商品 72 件.
已知购进甲种商品 x 件,则购进乙种商品件,根据题意,得
W=(130﹣120)x+(150﹣100)=﹣40x+10000,
∵k=﹣40<0,
∴W 随 x 的增大而减小.
∴当购进甲种商品的件数 x 逐渐增加时,利润 y 是逐渐减少的.
【点评】本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,一次函 数的性质的运用,解答时根据方程组的解求函数的解析式是关键.

练习册系列答案
相关题目
 x﹣
x﹣ 
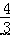 A.6 B.3 C.12 D.
A.6 B.3 C.12 D.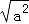 =﹣a,则实数 a 一定不在数轴原点右侧
=﹣a,则实数 a 一定不在数轴原点右侧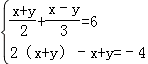
 A.﹣2015 B.
A.﹣2015 B. 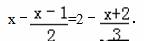
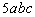 ,
,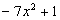 ,
,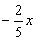 ,
,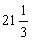 ,
,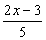 中,单项式共有
中,单项式共有