题目内容
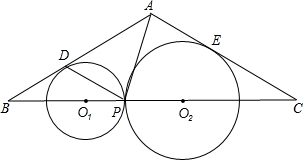
(2004•静安区二模)如图,在△ABC中,AB=AC=6,∠B=30°,点O1、O2在BC上,⊙O1与⊙O2外切于P,⊙O1与AB相切于点D,与AC相离,⊙O2与AC相切于E,与AB相离.
(1)求证:DP∥AC;
(2)设⊙O1的半径为x,⊙O2的半径为y,求y与x的函数解析式,并写出定义域;
(3)△ADP能否为直角三角形?如果能够,请求出⊙O2的半径;如果不能,请说明理由.
(1)求证:DP∥AC;
(2)设⊙O1的半径为x,⊙O2的半径为y,求y与x的函数解析式,并写出定义域;
(3)△ADP能否为直角三角形?如果能够,请求出⊙O2的半径;如果不能,请说明理由.

分析:(1)连接O1D,有切线的性质和已知条件证明∠DPO1=30°,再证明∠C=∠B=30°,进而证明∠DPO1=∠C,有同位角相等两线平行即可证明DP∥AC;
(2)连接O2E,作AH⊥BC,垂足为H,根据切线长定理和解直角三角形的知识即可求出求y与x的函数解析式,进而求出自变量的取值范围;
(3)△ADP能为直角三角形,此小题需要分当∠DPA=90°时;当∠DAP=90°时;当∠ADP=90°时,三种情况分别讨论,根据已知条件求出满足题意的半径值即可.
(2)连接O2E,作AH⊥BC,垂足为H,根据切线长定理和解直角三角形的知识即可求出求y与x的函数解析式,进而求出自变量的取值范围;
(3)△ADP能为直角三角形,此小题需要分当∠DPA=90°时;当∠DAP=90°时;当∠ADP=90°时,三种情况分别讨论,根据已知条件求出满足题意的半径值即可.
解答:(1)证明:连接O1D,
∵⊙O1与AB相切于点D,
∴∠BDO1=90°,
∵∠B=30°,
∴∠BO1D=60°,
∵O1D=O1P,
∴∠DPO1=∠PDO1,
∵∠DO1P=∠DPO1+∠PDO1=2∠DPO1,
∴∠DPO1=30°,
∵AB=AC,
∴∠C=∠B=30°.
∴∠DPO1=∠C,
∴DP∥AC;
(2)解:连接O2E,作AH⊥BC,垂足为H.
∵⊙O2与AC相切于E,∴∠CEO2=90°.
∵∠C=30°,PO2=EO2=y,∴CO2=2EO2=2y,
同理:PO1=x,BO1=2x.
在Rt△ABH中,BH=AB•cosB=6•coc60°=3
,
∴BC=2BH=6
,
∴2x+x+y+2y=6
∴函数解析式为y=2
-x,定义域为:
<x<
;
(3)解:△ADP能为直角三角形.
当∠DPA=90°时,∵DP∥AC,∴∠PAC=90°,
在Rt△APC中,CP=
=
=4
,
∴y+2y=4
,
∴y=
,
即⊙O2的半径为
,
当∠DAP=90°时,在Rt△ABP中,同理可求得x=
∴y=2
-
=
,
即⊙O2的半径为
,
由于∠ADO1=90°,所以∠ADP不可能为90°.
综上所述⊙O2的半径为
或
.
∵⊙O1与AB相切于点D,
∴∠BDO1=90°,

∵∠B=30°,
∴∠BO1D=60°,
∵O1D=O1P,
∴∠DPO1=∠PDO1,
∵∠DO1P=∠DPO1+∠PDO1=2∠DPO1,
∴∠DPO1=30°,
∵AB=AC,
∴∠C=∠B=30°.
∴∠DPO1=∠C,
∴DP∥AC;
(2)解:连接O2E,作AH⊥BC,垂足为H.
∵⊙O2与AC相切于E,∴∠CEO2=90°.
∵∠C=30°,PO2=EO2=y,∴CO2=2EO2=2y,
同理:PO1=x,BO1=2x.
在Rt△ABH中,BH=AB•cosB=6•coc60°=3
| 3 |
∴BC=2BH=6
| 3 |
∴2x+x+y+2y=6
| 3 |
∴函数解析式为y=2
| 3 |
| ||
| 2 |
3
| ||
| 2 |
(3)解:△ADP能为直角三角形.
当∠DPA=90°时,∵DP∥AC,∴∠PAC=90°,
在Rt△APC中,CP=
| AC |
| sinC |
| 6 |
| sin30° |
| 3 |
∴y+2y=4
| 3 |
∴y=
4
| ||
| 3 |
即⊙O2的半径为
4
| ||
| 3 |
当∠DAP=90°时,在Rt△ABP中,同理可求得x=
4
| ||
| 3 |
∴y=2
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
即⊙O2的半径为
2
| ||
| 3 |
由于∠ADO1=90°,所以∠ADP不可能为90°.
综上所述⊙O2的半径为
4
| ||
| 3 |
2
| ||
| 3 |
点评:本题综合考查了两圆外切的性质、两平行线的判定和性质、直角三角形的判定和直角三角形的性质以及解直角三角形的运用,题目综合性强难度大.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目