Question

【题目】中华鲟是国家一级保护动物，它是大型洄游性鱼类，生在长江，长在海洋，受生态环境的影响，数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量，每年放流的中华鲟中有少数体内安装了长效声呐标记，便于检测它们从长江到海洋的适应情况，这部分中华鲟简称为“声呐鲟”，研究所收集了它们到达下游监测点A的时间t（h）的相关数据，并制作如下不完整统计图和统计表．

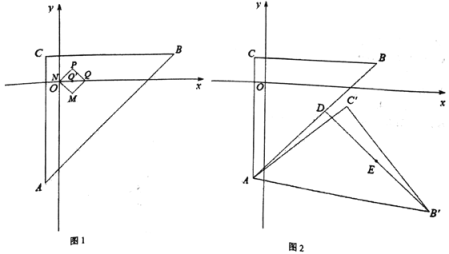
已知：今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A，今年落在24<t≤48内的“声呐鲟”比去年多1尾，今年落在48<t≤72内的数据分别为49，60，68，68，71．

去年20尾“声呐鲟”到达监测点A 所用时间t（h）的扇形统计图

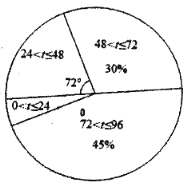
今年20尾“声呐鲟”到达监测点A所用时间t（h）的频数分布直方图

关于“声呐鲟”到达监测点A所用时间t（h）的统计表

	平均数	中位数	众数	方差
去年	64.2	68	73	715.6
今年	56.2	a	68	629.7

（1）请补全频数分布直方图，并根据以上信息填空：a= ；

（2）中华鲟到达海洋的时间越快，说明它从长江到海洋的适应情况就越好，请根据上述信息，选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好；

（3）去年和今年该放流点共放流1300尾中华鲟，其中“声呐鲟”共有50尾，请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A．

Answer 1

【答案】（1）64；（2）见详解；（3）1560

【解析】

（1）先求出去年落在48＜t≤72内的数据个数，从而根据“今年落在24＜t≤48内的“声呐鲟”比去年多1尾”得到今年落在48＜t≤72内的数据个数，继而根据各时间段的数据和为20求出24＜t≤48内的数据个数，从而补全图形，最后根据中位数的概念求解可得；

（2）从平均数上看去年“声呐鲟”到达下游监测点的平均时间为64.2小时，而今年“声呐鲟”到达下游监测点的平均时间为56.2小时，缩短了8小时，答案不唯一，合理即可；

（3）用总数量乘以放流72小时内通过监测站A的对应的百分比求出去年、今年的数量，求和即可得．

解：（1）去年落在48＜t≤72内的数据有20×（个），

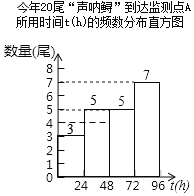
∴今年落在48＜t≤72内的数据为5，

则今年24＜t≤48内的“声呐鲟”数量为20-（5+5+7）=3，

补全图形如下：

∵今年“声呐鲟”到达下游监测点时间的第10、11个数据为60、68，

∴a=，

故答案为：64．

（2）选择平均数，

由表可知，去年“声呐鲟”到达下游监测点的平均时间为64.2小时，而今年“声呐鲟”到达下游监测点的平均时间为56.2小时，缩短了8小时，

所以今年“声呐鲟”从长江到海洋的适应情况更好（答案不唯一，合理即可）．

（3）去年和今年在放流72小时内中华鲟通过监测站A的数量为

1300×（1-45%）+1300×=715+845=1560（尾）．