题目内容
 如图,已知∠AOB是直角,∠AOC=46°,OM平分∠AOC,ON平分∠BOC,
如图,已知∠AOB是直角,∠AOC=46°,OM平分∠AOC,ON平分∠BOC,(1)试求∠MON的度数;
(2)当∠AOC的大小在10°~90°之间变化时,请问∠MON的大小是否变化?并说明理由.
考点:角的计算,角平分线的定义
专题:计算题
分析:(1)先求出∠BOC,再根据角平分线的定义求出∠NOC、∠MOC,然后根据∠MON=∠NOC-∠MOC代入数据进行计算即可得解;
(2)根据(1)中思路求解即可.
(2)根据(1)中思路求解即可.
解答:解:(1))∵∠AOB是直角,∠AOC=46°,
∴∠BOC=∠AOB+∠AOC=90°+46°=136°,
∵ON平分∠BOC,
∴∠NOC=
∠BOC=
×136°=68°,
∵OM平分∠AOC,
∴∠MOC=
∠AOC=
×46°=23°,
∴∠MON=∠NOC-∠MOC=68°-23°=45°;
(2)∠MON=45°,∠MON不会变,理由如下:
∠MON=∠AOM+∠AON
=
∠AOC+∠AOB-∠BON
=
∠AOC+∠AOB-
∠BOC
=∠AOB-
(∠BOC-∠AOC)
=∠AOB-
∠AOB
=
∠AOB
=45°.
∴∠BOC=∠AOB+∠AOC=90°+46°=136°,
∵ON平分∠BOC,
∴∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵OM平分∠AOC,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠NOC-∠MOC=68°-23°=45°;
(2)∠MON=45°,∠MON不会变,理由如下:
∠MON=∠AOM+∠AON
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=∠AOB-
| 1 |
| 2 |
=∠AOB-
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°.
点评:本题考查了角的计算,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
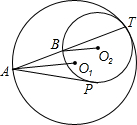 如图,⊙O1与⊙O2内切于点T,⊙O1的弦AT交⊙O2于点B,AP切⊙O2于点P,连接AO1、BO2.证明:
如图,⊙O1与⊙O2内切于点T,⊙O1的弦AT交⊙O2于点B,AP切⊙O2于点P,连接AO1、BO2.证明: 用图象法解二元一次方程组:
用图象法解二元一次方程组: 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的-x2+2x+m=0一元二次方程的解为
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的-x2+2x+m=0一元二次方程的解为