题目内容
19.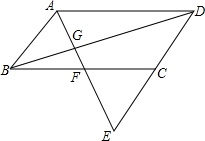 如图,已知?ABCD,E是DC延长线上一点.AE交BD于点G、交BC于点F.
如图,已知?ABCD,E是DC延长线上一点.AE交BD于点G、交BC于点F.(1)求证:AG2=EG•FG;
(2)若AG=6,FG=4,求EF的长;
(3)求证:DG2:BG2=EG:FG.
分析 (1)运用平行四边形的性质证明△ADG∽△EBG,△DGF∽△BGA,列出比例式进行比较、分析、归纳、总结,即可解决问题;
(2)由(1)知AG2=EG•FG,把AG=6,FG=4代入,即可求得结果;
(3)由(1)AG:GE=BG:DG,两边平方得AG2:GE2=BG2:DG2,由于AG2=EG•FG;代入即可求得结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DE,AD∥BF;
∴△ABG∽△EDG,△BGF∽△DGA,
∴AG:GE=BG:DG,FG:AG=BG:DG,
∴AG:EG=FG:AG,
∴AG2=EG•FG;
(2)解:由(1)知AG2=EG•FG,
∵AG=6,FG=4,
∴EG=9,
∴EF=5;
(3)证明:由(1)AG:GE=BG:DG,
∴AG2:GE2=BG2:DG2,
∵AG2=EG•FG;
∴DG2:BG2=EG:FG.
点评 本题主要考查了平行四边形的性质、相似三角形的判定与性质、等量代换,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列方程中是一元二次方程的是( )
| A. | 2+$\frac{5}{{x}^{2}}$=0 | B. | x+2y=3 | C. | 3x=2x2-1 | D. | x2-3y+2=0 |
4.下列函数中,自变量x的取值范围是x>2的函数是( )
| A. | y=x-2 | B. | y=x2-4 | C. | y=$\frac{1}{x-2}$ | D. | y=$\frac{1}{{\sqrt{x-2}}}$ |
8.a,b互为相反数,下列结论中不一定正确的是( )
| A. | 5a+5b=0 | B. | a÷b=-1 | C. | ab≤0 | D. | |a|=|b| |





 如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.
如图.已知点A(1,2)、B(4,1)、C(8,3).利用坐标网格和你的观察力.请直按说出△ABC外心的坐标和外接圆半径.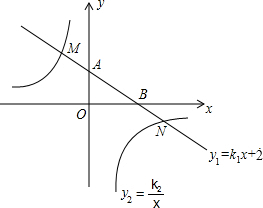 在平面直角坐标系xOy中,一次函数y1=k1x+2的图象与y轴交于点A,与x轴交于点B,与反比例函数y2=$\frac{k_2}{x}$的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.
在平面直角坐标系xOy中,一次函数y1=k1x+2的图象与y轴交于点A,与x轴交于点B,与反比例函数y2=$\frac{k_2}{x}$的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.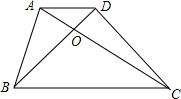 如图所示,梯形ABCD中,AD∥BC,对角线AC和BD相交于点O,若S△AOD:S△ACD=1:3.求S△AOD:S△BOC.
如图所示,梯形ABCD中,AD∥BC,对角线AC和BD相交于点O,若S△AOD:S△ACD=1:3.求S△AOD:S△BOC.