题目内容
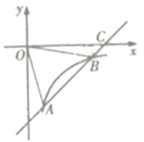
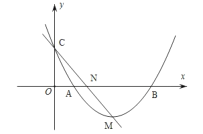
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,抛物线
轴正半轴上,抛物线![]() 经过
经过![]() 、
、![]() 两点,连接
两点,连接![]() ,
,![]() .
.
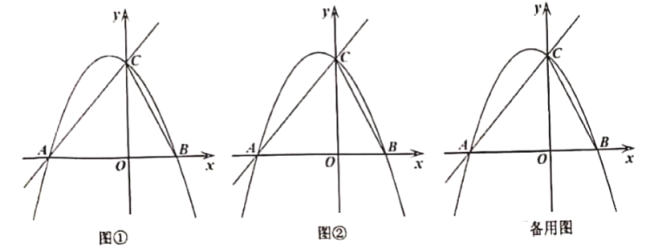
(1)求抛物线的解析式:
(2)点![]() 在第二象限的抛物线上,过点
在第二象限的抛物线上,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,若点![]() 和点
和点![]() 同在一个象限内,连接
同在一个象限内,连接![]() 、
、![]() ,
,![]() ,求
,求![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点M的坐标为
;(3)点M的坐标为![]() 或
或![]()
【解析】
(1)根据直线![]() 求出A,C的坐标,再根据面积求出B点坐标,即可求出解析式;
求出A,C的坐标,再根据面积求出B点坐标,即可求出解析式;
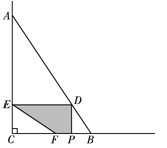
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交
,交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,表示出OE和OF的长,根据矩形的性质表示出PF,即可列等式解出n,从而求出PD;
,表示出OE和OF的长,根据矩形的性质表示出PF,即可列等式解出n,从而求出PD;
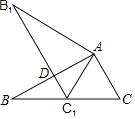
(3)分情况讨论,①当点![]() 在点
在点![]() 上方时,②当点
上方时,②当点![]() 在点
在点![]() 下方时,作出辅助线,根据
下方时,作出辅助线,根据![]() 求出
求出![]() 点坐标即可.
点坐标即可.
(1)直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
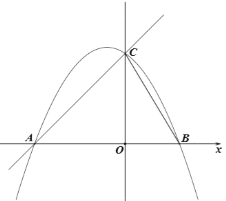
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∵抛物线![]() 经过
经过![]() 两点,
两点,
∴![]() ,
,
解得: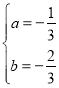 ,
,
∴抛物线解析式为:![]() ;
;
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交
,交![]() 于点
于点![]() ,
,
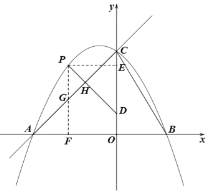
设点![]() 的横坐标为
的横坐标为![]() ,
,
则纵坐标为:![]() ,
,
![]() ,
,
![]() ,
,
在矩形![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() (舍去),
(舍去),
∵点![]() 在第二象限的抛物线上,
在第二象限的抛物线上,
![]() ,
,
![]() ;
;
(3)![]() ,
,
∴点![]() 在直线
在直线![]() 上 ,
上 ,
![]() ,
,
![]() ,
,
∴点![]() 也在直线
也在直线![]() 上,
上,
①当点![]() 在点
在点![]() 上方时,过点
上方时,过点![]() 作
作![]() 于点
于点![]() ,
,
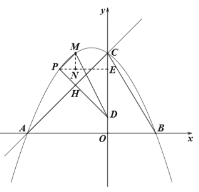
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
②当点![]() 在点
在点![]() 下方时,过点
下方时,过点![]() 作
作![]() 延长线于点
延长线于点![]() ,
,
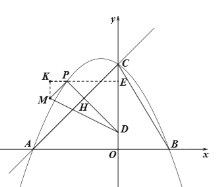
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点M的坐标为![]() 或
或![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目