题目内容
16.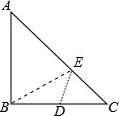 如图,Rt△ABC中,AB=BC=2,D为BC的中点,在AC边上存在一点E,连接ED,EB,则EB+ED的最小值为( )
如图,Rt△ABC中,AB=BC=2,D为BC的中点,在AC边上存在一点E,连接ED,EB,则EB+ED的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{2}+1$ | C. | $\sqrt{5}$ | D. | $2\sqrt{2}$ |
分析 由等腰直角三角形补全正方形,找B′C的中点D′,通过证明三角形全等找出ED=ED′,再由三角形内两边之和大于第三边得出当B、E、D′三点共线时,EB+ED′最小,由勾股定理可在Rt△BCD′中求出BD′的值,从而得出结论.
解答 解:将等腰直角三角形补充成正方形,其中B点与B′点相对,取B′C的中点D′,连接D′B交AC于点E,如图所示.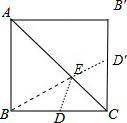
∵四边形ABCB′为正方形,且D为BC中点,D′为B′C中点,
∴DC=D′C,∠DCE=∠D′CE=45°,
即在△DCE与△D′CE中,有$\left\{\begin{array}{l}{DC=D′C}\\{∠DCE=∠D′CE}\\{EC=EC}\end{array}\right.$,
∴△DCE≌△D′CE,
∴ED=ED′.
当B、E、D′三点共线时,EB+ED′最小(三角形内边之和大于第三边).
在Rt△BCD′中,BC=2,CD′=$\frac{1}{2}$BC=1,∠BCD′=90°,
由勾股定理可知:BD′=$\sqrt{B{C}^{2}+CD{′}^{2}}$=$\sqrt{5}$.
故选C.
点评 本题考查了正方形的性质、轴对称-最短线路问题,解题的关键是找出ED′=ED.本题属于基础题,在求最短线路中也是属于简单题的存在,解决该类问题一般都是找到其中一个点关于直线的对称点再连接,该题巧合在三角形为等腰直角三角形,故只需补充成正方形即可.

练习册系列答案
相关题目
7.下列各组单项式中,不是同类项的是( )
| A. | 3x2y与-2yx2 | B. | 2ab2与-ba2 | C. | $\frac{xy}{3}$与5xy | D. | 23a与32a |
4.正方形两条对角线之和为8cm,则它的面积为( )
| A. | 8 | B. | $4\sqrt{2}$ | C. | 4 | D. | 16 |
1.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.6.(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)=0.6.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{b}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(白球)=0.6.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
5.下列各组线段中,不成比例的是( )
| A. | 4cm、6cm、8cm、10cm | B. | 4cm、6cm,8cm、12cm | ||
| C. | 11cm、22cm、33cm、66cm | D. | 2cm、4cm、4cm、8cm |
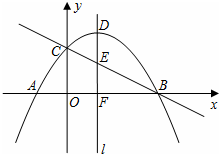 如图,抛物线y=-$\frac{1}{4}$x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E,与x轴相交于点F.
如图,抛物线y=-$\frac{1}{4}$x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E,与x轴相交于点F.