Question

如图，正比例函数y₁=k₁x的图象与反比例函数的图象相交于A、B两点，其中点A的坐标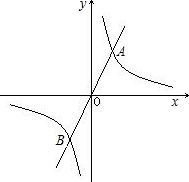为（1，2）．
（1）分别求出这两个函数的表达式；
（2）请你观察图象，写出y₁＞y₂时，x的取值范围；
（3）在y轴上是否存在点P，使△AOP为等腰三角形？若存在，请你直接写出点P的坐标；若不存在，请说明理由．

Answer 1

分析：（1）设直线方程为y₁=k₁x，反比例函数y=

k2

x

，两图象都经过点A，解得k₁和k₂，
（2）解得两交点的坐标，观察图象写出x的取值范围，
（3）存在4种情况的点P，OP为腰和底两种情况，分别求出OP．

解答：（1）解：∵y₁=k₁x过点A（1，2），
∴k₁=2．（2分）
∴正比例函数的表达式为y₁=2x．（3分）
∵反比例函数过点A（1，2），
∴k₂=2．（5分）
∴反比例函数的表达式为y=

2

x

．（6分）

（2）-1＜x＜0或x＞1．（8分）

（3）∵点A的坐标为（1，2），
∴OA=

5

，
当OA为腰时，OA=OP₂=

5

，P₂点坐标为（0，4），
当AP₁=OA=

5

，可知P₁坐标为（0，

5

），
当OA=OP₃=

5

时，可得P₃坐标为（0，-

5

）
由图可知，P₁（0，

5

），P₂（0，-

5

），P₃（0，-4），
当OA为底时，OP₄=

1 2 OA

cosAOP4

=

5

4

，
可知P₄（0，

5

4

），
故P₁（0，

5

），P₂（0，-

5

），P₃（0，-4），P₄（0，

5

4

）．（12分）

点评：本题主要考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=

k

x

中k的几何意义．这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．