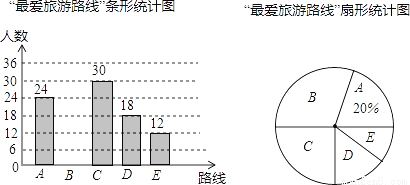
题目内容
如图,在边长为4的正方形ABCD中,P是BC边上一动点(不与B、C两点重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上取一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接AM、AN.
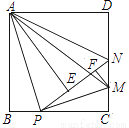
(1)若P为BC的中点,则sin∠CPM=________;
(2)求证:∠PAN的度数不变;
(3)当P在BC边上运动时,△ADM的面积是否存在最小值,若存在,请求出PB的长;若不存在,请说明理由.
(1);(2)证明见解析;(3)存在最小值,BP=2. 【解析】试题分析:(1)根据正方形的性质和勾股定理求出AP,根据正弦的定义得到sin∠BAP=,根据折叠的性质证明∠CPM=∠BAP,得到答案; (2)证明Rt△AEN≌Rt△ADN,得到∠EAN=∠DAN,计算即可; (3)设PB=x,根据相似三角形的性质求出DM,根据三角形的面积公式得到二次函数的解析式,然后将解析式转化...
练习册系列答案
相关题目


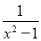 )÷
)÷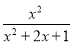 ,其中x=
,其中x= 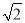 +1.
+1.