题目内容
5.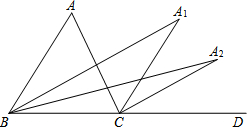 如图所示,△ABC中,外角∠ACD的平分线与∠ABC的平分线交于A1,∠A1BC与∠A1CD的平分线交于A2,则:
如图所示,△ABC中,外角∠ACD的平分线与∠ABC的平分线交于A1,∠A1BC与∠A1CD的平分线交于A2,则:(1)∠A2与∠A有怎样的数量关系?写出并证明;
(2)继续作∠A2BC与∠A2CD的平分线可得∠A3,如此下去可得∠A4,…,∠An,猜想∠An=$\frac{1}{{2}^{n}}$∠A;
(3)当∠A=64°时,∠A4=4°.
分析 (1)根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的$\frac{1}{2}$,
(2)根据发现后一个角等于前一个角的$\frac{1}{2}$的规律即可得解,
(3)把∠A=64°代入∠An=$\frac{1}{{2}^{n}}$∠A解答即可.
解答 解:(1)∠A2=$\frac{1}{4}∠A$,理由如下:
∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠ABC+∠A1,
∴∠A1=$\frac{1}{2}$∠A,
同理可得∠A2=$\frac{1}{2}$∠A1=$\frac{1}{2}•\frac{1}{2}∠A$=$\frac{1}{4}∠A$,
(2)根据以上规律∠An=$\frac{1}{{2}^{n}}$∠A,
故答案为:$\frac{1}{{2}^{n}}$;
(3)当∠A=64°时,∠A4=$\frac{1}{{2}^{4}}×64°=4°$,
故答案为:4°.
点评 本题考查的是三角形内角和定理,根据角平分线的定义可得∠A1BC=$\frac{1}{2}$∠ABC,∠A1CD=$\frac{1}{2}$∠ACD是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.-7+13-6+20可以表示几个数的和,这几个数分别是( )
| A. | -7,13,6,20 | B. | 7,13,-6,20 | C. | -7,13,-6,-20 | D. | -7,13,-6,20 |
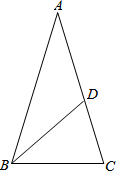 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC. 已知有理数a、b、c在数轴上的位置如图所示,在数轴上分别找出与表示有理数α、b、c的点到原点0距离相等的点.
已知有理数a、b、c在数轴上的位置如图所示,在数轴上分别找出与表示有理数α、b、c的点到原点0距离相等的点.