题目内容
 如图,在四边形草坪ABCD中,∠A=∠C=90°,AB=30米,AD=40米,BC=DC,求四边形草坪ABCD的面积.
如图,在四边形草坪ABCD中,∠A=∠C=90°,AB=30米,AD=40米,BC=DC,求四边形草坪ABCD的面积.考点:勾股定理
专题:
分析:连接BD,先根据勾股定理求出BD的长,然后将两个直角三角形的面积相加即为四边形ABCD的面积.
解答: 解:连结BD,在Rt△ABD中,BD2=AB2+AD2=302+402=502,所以BD=50.
解:连结BD,在Rt△ABD中,BD2=AB2+AD2=302+402=502,所以BD=50.
在Rt△BCD中,因为BC=DC,
所以BC2=DC2=
BD2=
×502=1250,
所以BC•CD=1250.S四边形ABCD=S△ABD+S△BCD=
AB•AD+
BC•CD=
×30×40+
×1250=1825(平方米).
所以四边形草坪ABCD的面积为1825平方米.
 解:连结BD,在Rt△ABD中,BD2=AB2+AD2=302+402=502,所以BD=50.
解:连结BD,在Rt△ABD中,BD2=AB2+AD2=302+402=502,所以BD=50.在Rt△BCD中,因为BC=DC,
所以BC2=DC2=
| 1 |
| 2 |
| 1 |
| 2 |
所以BC•CD=1250.S四边形ABCD=S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以四边形草坪ABCD的面积为1825平方米.
点评:此题主要考查勾股定理和勾股定理的逆定理等知识点,难度不大,此题的突破点是连接BD,求出两个三角形的面积,二者相加即可.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
在等式y=kx+b中,当x=1时,y=2;当x=2时,y=-4,则式子3k+2b的值为( )
| A、-34 | B、-2 | C、34 | D、2 |
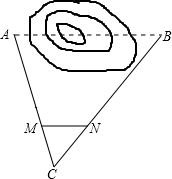 如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )
如图,A、B两点被池塘隔开,在AB外任取一点C,连结AC、BC分别取其三等分点M,N(M、N两点均靠近点C).量得MN=27m,则AB的长是( )| A、54m | B、81m |
| C、108m | D、135m |
 如图,在△ABC中,D、E分别是AB、AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=
如图,在△ABC中,D、E分别是AB、AC的中点,F是BC延长线上的一点,FC=3,DF交CE于点G,且EG=CG,则BC=