题目内容
12.如图,点A(1,$\sqrt{3}$),将线段OA平移至线段BC,B(3,0).(1)请直接写出点C的坐标;
(2)连AC,AB,求三角形ABC的面积;
(3)若∠AOB=60°,点P为y轴上一动点(点P不与原点重合),试探究∠CPO与∠BCP之间的数量关系并证明你的结论.
分析 (1)由平移得到BM=BN=$\sqrt{3}$,从而得出点C坐标;
(2)由平移得到四边形OABC是矩形,△ABC的面积和△OAB的面积一样大,
(3)分三种情况讨论计算,①当点P在y轴负半轴时,BC与y轴交点(含交点)上方时.②当点P在y轴负半轴时,BC与y轴交点(含交点)下方时,③当点P在y轴正半轴时,简单计算即可.
解答 解:(1)如图,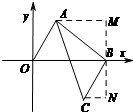
∵点A(1,$\sqrt{3}$),将线段OA平移至线段BC,B(3,0).
∴BM=BN=$\sqrt{3}$,
∴C(2,-$\sqrt{3}$);
(2)连接OC,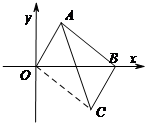
∵B(3,0)
∴OB=3,
由平移得,四边形OABC是矩形,
S三角形ABC=S三角形OBC=$\frac{1}{2}$OB×|yC|=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$;
(3)过点P作直线l∥AO,
∵OA∥BC,
∴l∥BC,
①如图,
当点P在y轴负半轴时,BC与y轴交点(含交点)上方时.
∠CPO+∠BCP=360°-90°-60°=210°
②如图,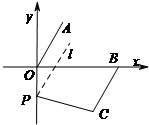
当点P在y轴负半轴时,BC与y轴交点(含交点)下方时.
∠BCP-∠CPO=150°
③当点P在y轴正半轴时,
∠BCP-∠CPO=∠AOy=90°-60°=30°
点评 此题是几何变换综合题,主要考查了平移的性质,三角形面积的计算,分类讨论计算,解本题的关键是分类,易漏掉.

练习册系列答案
相关题目
2.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,
以下说法正确的是( )
| 劳动时间(小时) | 3 | 4 | 5 | 6 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是5,平均数是3.6 | B. | 众数是5,平均数是4.6 | ||
| C. | 中位数是4,平均数是3.6 | D. | 众数是2,平均数是4.6 |
17.下列四个算式:①a6•a6=a6;②m3+m2=m5;③x2•x•x8=x10;④y2+y2=y4.其中计算正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
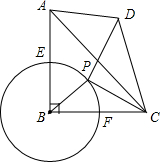 如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.
如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.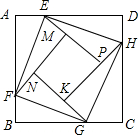 如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
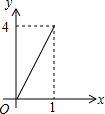

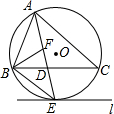 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.