Question

【题目】如图，已知自行车与摩托车从甲地开往乙地，OA与BC分别表示它们与甲地距离s（千米）与时间t（小时）的关系，则：

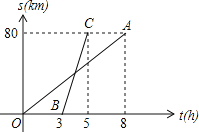
（1）摩托车每小时走　 　千米，自行车每小时走　 　千米；

（2）自行车出发后多少小时，它们相遇？

（3）摩托车出发后多少小时，他们相距10千米？

Answer 1

【答案】（1）40，10；（2）4小时；（3）摩托车出发后或或4小时，他们相距10千米

【解析】

（1）根据图像可得BC为摩托车的图像可得时间和路程，就可以得到摩托车的速度；OA为自行车图像，由图像可得时间和路程，就可以得到自行车的速度；

（2）由图像可知自行车先出发3小时，由相遇时两车路程相等可列方程。

（3）由相遇前自行车在摩托车前，可用自行车路程－摩托车路程=10；

相遇后摩托车在自行车前，可用摩托车路程－自行车路程=10

最后摩托车达到终点不再行驶，则自行车距离终点10千米也为题中所求

（1）摩托车每小时走：80÷（5﹣3）＝40（千米），

自行车每小时走：80÷8＝10（千米）．

故答案为：40，10；

（2）设自行车出发后x小时，它们相遇，

10x＝40（x﹣3）

解得x＝4．

（3）设摩托车出发后t小时，他们相距10千米；

①相遇前：10（t+3）﹣40t＝10，

解得t＝；

②相遇后：40t﹣10（t+3）＝10，

解得：t＝，

③摩托车到达终点10（t+3）＝70，解得t＝4

答：摩托车出发后或或4小时，他们相距10千米．