题目内容
关于x的一元二次方程x2+ax-5=0的两个实数根分别是x1,x2,若x1+x2=4,则a= ,|x1-x2|= .
考点:根与系数的关系
专题:
分析:根据根与系数的关系得到x1+x2=-a=4,求得a,然后可分别计算出x1、x2的值,进一步求得答案即可.
解答:解:∵一元二次方程x2+ax-5=0的两个实数根分别是x1,x2,
∴x1+x2=-a=4,
∴a=-4,
则方程x2-4x-5=0的两个实数根分别是x1=5,x2=-1,
∴,|x1-x2|=6.
故答案为:-4;6.
∴x1+x2=-a=4,
∴a=-4,
则方程x2-4x-5=0的两个实数根分别是x1=5,x2=-1,
∴,|x1-x2|=6.
故答案为:-4;6.
点评:此题考查根与系数的关系,解答此题的关键是熟知一元二次方程根与系数的关系:x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
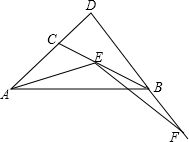 如图,△ABD中,C是AD上的一点,且AD=k•DB,DB=k•DC,AC=m•BC,E是直线BC上一点,∠AEF=∠ACB,EF交直线DB于F,试探究AE与EF之间的数量关系.
如图,△ABD中,C是AD上的一点,且AD=k•DB,DB=k•DC,AC=m•BC,E是直线BC上一点,∠AEF=∠ACB,EF交直线DB于F,试探究AE与EF之间的数量关系. 已知一次函数y=kx+b的图象如图所示,不等式kx+b<0的解集是
已知一次函数y=kx+b的图象如图所示,不等式kx+b<0的解集是