题目内容
直线y=
x向左平移3个单位交y轴于点B,交反比例函数y=
的图象于点A,若OA=
BO,则k的值是 .
| 2 |
| 3 |
| k |
| x |
| 5 |
| 2 |
考点:反比例函数与一次函数的交点问题,一次函数图象与几何变换
专题:计算题
分析:直线y=
x向左平移3个单位交x轴于点C,作AD⊥x轴于D,如图,则C(0,-3),根据一次函数的几何变换可设直线AC的解析式为y=
x+b,把C(-3,0)代入可计算出b=2,则直线AC的解析式为y=
x+2,得到B点坐标为(0,2),利用OA=
BO得到OA=5,设A(x,
x+2),利用勾股定理得到x2+(
x+2)2=52,解得x1=3,x2=-
,易得A点坐标为(3,4),然后把A(3,4)代入y=
可计算出k的值.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 63 |
| 13 |
| k |
| x |
解答:解: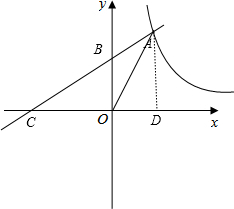 直线y=
直线y=
x向左平移3个单位交x轴于点C,作AD⊥x轴于D,如图,则C(0,-3),
设直线AC的解析式为y=
x+b,
把C(-3,0)代入得
×(-3)+b=0,解得b=2,
∴直线AC的解析式为y=
x+2,
∴B点坐标为(0,2),
∵OA=
BO,
∴OA=5,
设A(x,
x+2),
在Rt△AOD中,∵OD2+AD2=OA2,
∴x2+(
x+2)2=52,
整理得13x2+24x-189=0,
解得x1=3,x2=-
,
当x=3时,y=
x+2=4,
∴A点坐标为(3,4),
把A(3,4)代入y=
得k=3×4=12.
故答案为12.
 直线y=
直线y=| 2 |
| 3 |
设直线AC的解析式为y=
| 2 |
| 3 |
把C(-3,0)代入得
| 2 |
| 3 |
∴直线AC的解析式为y=
| 2 |
| 3 |
∴B点坐标为(0,2),
∵OA=
| 5 |
| 2 |
∴OA=5,
设A(x,
| 2 |
| 3 |
在Rt△AOD中,∵OD2+AD2=OA2,
∴x2+(
| 2 |
| 3 |
整理得13x2+24x-189=0,
解得x1=3,x2=-
| 63 |
| 13 |
当x=3时,y=
| 2 |
| 3 |
∴A点坐标为(3,4),
把A(3,4)代入y=
| k |
| x |
故答案为12.
点评:本题考查了反比例函数与一次函数的交点:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了一次函数图象与几何变换.

练习册系列答案
相关题目
太阳直径为1 390 000km,用科学记数法表示为( )km.
| A、1.39×106 |
| B、13.9×105 |
| C、1.39×107 |
| D、0.139×108 |
某城市计划经过两年时间,将城市绿地面积从今年的1000000平方米提高到1440000平方米,则每年的平均增长是( )
| A、15% | B、20% |
| C、25% | D、30% |