题目内容
1．△ABC中，AB=AC=4，∠B=15°，则△ABC的面积为（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
分析 据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD的度数，然后根据30°角所对的直角边等于斜边的一半求解即可．
解答 
解：过C作CD⊥AB交BA的延长线于D，
∵AB=AC=4，∴∠B=∠ACB=15°，
∴∠CAD=∠B+∠ACB=15°+15°=30°，
∵AC=4cm，CD是AB边上的高，
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2，
∴S△ABC=$\frac{1}{2}$×4×2=4，
故选A．
点评 本题考查了30°角所对的直角边等于斜边的一半的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟练掌握性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
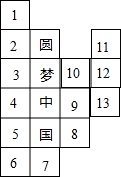从下图中的正方形中选两个涂色，使这两个正方形与4个写有汉字的正方形一起，折叠后能围成一个正方体，则你所涂的正方形是2和9（只填数字即可）．
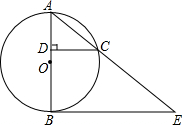如图，AB是⊙O的直径，C是⊙O上一点，CD⊥AB，垂足为D，过点B作直线BE∥DC，交AC的延长线于点E．
如图，∠AOB，∠BOC，∠AOC的大小关系用“＞”连接起来：∠AOC＞∠AOB＞∠BOC．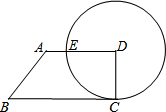
如图，已知四边形ABCD中，AD∥BC，∠C=90°，∠B=45°，以D为圆心，DC为半径的圆交AD于点E．若AB=2$\sqrt{2}$，AD=2$\sqrt{3}$，判断直线AB与⊙D位置关系，并说明理由．
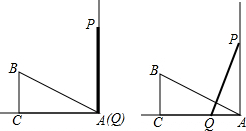已知墙面与地面成直角，直角△ABC如图放置，BC=3cm，AC=4cm，AB=5cm，一木棒PQ靠在墙上，且PQ=5cm．木棒沿墙面滑下（P向A运动，Q向C运动），P点运动到A点就停止运动，已知P点的运动速度是1cm/s，当P运动1或2s时，△ABC与△PQA全等．