题目内容
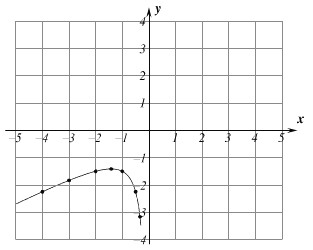
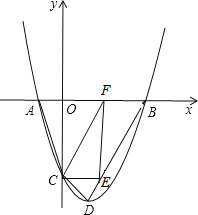
【题目】如图所示，二次函数
的图象与
轴交于点
、
，与
轴交于点
，直线
经过点、．
（1）求抛物线的表达式；
（2）过点的直线
交抛物线于点
，交直线
于点
，连接
，当直线平分
的面积时，求点的坐标；
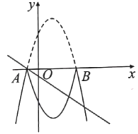
（3）如图所示，把抛物线位于轴上方的图象沿轴翻折，当直线与翻折后的整个图象只有三个交点时，求
的取值范围．
【答案】（1）
；（2）
；（3）
．
【解析】
（1）根据已知条件求出B、C两个点的坐标，再把这两个点的坐标代入二次函数即可求出抛物线的解析式；
（2）根据题意画出图形根据三角形的面积即可求解；
（3）先求出翻折后的抛物线解析式，再利用抛物线与直线相交的特点即可求解．
（1）令直线
，x=0,得y=4
令y=0,则-x+4=0，解得x=4
∴点
、
的坐标分别为
、
，
把点、的坐标分别代入
，
得
，
解得
抛物线的表达式为：．
（2）令=0，
解得x1=-1,x2=4,
∴
，
如图所示，过点
作
于
，
直线
平分
的面积，
，
当
时，
，
把
代入，得
，
直线
的解析式为
，
由
解得
，
；
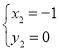
（3）∵=
，故顶点坐标为（
，
）
∴翻折后的抛物线的顶点坐标为（，-）
∴翻折后的抛物线为
=
，
∴翻折后的整个图象包括两部分：分别是：
抛物线y＝x23x4（1≤x≤4）和y＝x2＋3x＋4（x＞4或x＜1）．
①当直线y＝kx＋k与抛物线x23x4＝（1≤x≤4）相交时，
由
，得x23x4＝kx＋k，
整理，得x2（k＋3）x（k＋4）＝0
解得x1＝1，x2＝k＋4．
所以y1＝0，y2＝k2＋5k．
所以两个函数图象有两个交点，
其中一个交点为A（1，0），另一个交点坐标为（k＋4，k2＋5k）．
观察图象可知：另一个交点在x轴下方，横坐标在1与4之间，纵坐标在与0之间．
所以1＜k＋4＜4，解得5＜k＜0．
＜k2＋5k＜0，整理，得
4k2＋20k＋25＞0或k2＋5k＜0，
解得，（2k＋5）2＞0或5＜k＜0．
k为任意实数，（2k＋5）2＞0都成立，
所以5＜k＜0；
②当直线y＝kx＋k与图象y＝x2＋3x＋4（x＞4，或x＜1）相交时，
x2＋3x＋4＝kx＋k，
整理得x2＋（k3）x＋（k4）＝0
解得x1＝1，x2＝4k，
所以y1＝0，y2＝5kk2．
所以两个函数图象有两交点，
其中一个是点A（1，0），另一个交点坐标为（4k，5kk2）．
观察图象可知：另一个交点的横坐标大于4，纵坐标小于0，
即4k＞4，解得k＜0．
5kk2＜0，
∴k（5k）＜0，
∵k＜0，
∴5k＞0，
∴k＜5
∴k＜0
∴综上所述：当直线y＝kx＋k与翻折后的整个图象只有三个交点时，k的取值范围是：5＜k＜0．
