题目内容
【题目】小林在学习完一次函数与反比例函数的图象与性质后,对函数图象与性质研究饶有兴趣,便想着将一次函数与反比例函数的解析式进行组合研究.他选取特殊的一次函数![]()
![]() 与反比例函数
与反比例函数![]()
![]() ,相加后,得到一个新的函数
,相加后,得到一个新的函数![]()
![]() .已知,这个新函数满足:当
.已知,这个新函数满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求出小林研究的这个组合函数的解析式;
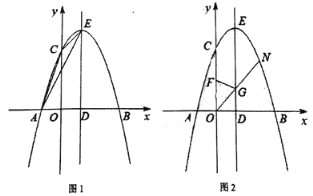
(2)小林依照列表、描点、连线的方法在给定的平面直角坐标系内画出了该函数图象的一部分,请你在图中补全小林未画完的部分,并根据图象,写出该函数图象的一条性质;
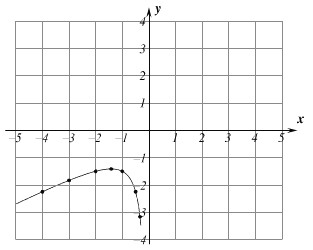
(3)请根据你所画的函数图象,利用所学函数知识,直接写出不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)见解析,函数图象关于原点
;(2)见解析,函数图象关于原点![]() 成中心对称;(3)
成中心对称;(3)![]() 或
或![]()
【解析】
(1)将已知数据![]() 时,
时,![]() ;
; ![]() 时,
时,![]() 代入新函数关系式,求解即可;
代入新函数关系式,求解即可;
(2)通过已知函数图象补全图象,观察图象可得到图象性质;
(3)画出函数![]() 的图象,找到函数
的图象,找到函数![]() 的图象不低于函数
的图象不低于函数![]() 图象时对应的x范围即可.
图象时对应的x范围即可.
解:(1)将![]() ,
,![]() 代入
代入![]()
可得
解得:
∴![]()
(2)所画图象如图所示
函数性质:函数图象关于原点![]() 成中心对称
成中心对称

(3)画出函数![]() 图象如图,
图象如图,

由图象可知,当![]() 时,
时,![]() 或
或![]()

练习册系列答案
相关题目