题目内容
梯形中位线长为10，高为5，则梯形面积为 ．
考点：梯形中位线定理
专题：
分析：根据梯形的面积等于其中位线×高，即可求得其面积．
解答：解：∵梯形的面积=中位线×高，
∴面积=10×5=50．
故答案为50．
∴面积=10×5=50．
故答案为50．
点评：本题考查了梯形的中位线定理及梯形的面积计算方法，梯形的中位线等于两底和的一半，据此可以解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
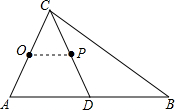如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5，CD是斜边AB上的中线，以AC为直径作⊙O，设线段CD的中点为P，则点P与⊙O的位置关系是（ ）| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
已知⊙A是以（-1，2）为圆心，1为半径的圆，则下列说法正确的是（ ）
| A、⊙A必与x轴相交 |
| B、⊙A必与x轴相切 |
| C、⊙A必与y轴相交 |
| D、⊙A必与y轴相切 |
以下命题中，真命题的是（ ）
| A、两条直线只有相交和平行两种位置关系 |
| B、同位角相等 |
| C、两边和一角对应相等的两个三角形全等 |
| D、等腰三角形底边中点到两腰的距离相等 |