题目内容
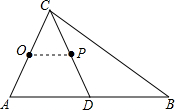 如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5,CD是斜边AB上的中线,以AC为直径作⊙O,设线段CD的中点为P,则点P与⊙O的位置关系是( )| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、无法确定 |
考点:点与圆的位置关系
专题:
分析:先利用中线得到AD=
AB=
,再证明OP为△CAD的中位线,得到OP=
,然后比较OP与半径的大小后根据点与圆的位置关系进行判断.
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
解答:解:∵CD是斜边AB上的中线,
∴AD=
AB=
,
∵点O为AC的中点,P为CD的中点,
∴OP为△CAD的中位线,
∴OP=
AD=
,
而AC为⊙O的直径,即半径为
,
∴点P到圆心O的距离小于圆的半径,
∴点P在⊙O内.
故选A.
∴AD=
| 1 |
| 2 |
| 5 |
| 2 |
∵点O为AC的中点,P为CD的中点,
∴OP为△CAD的中位线,
∴OP=
| 1 |
| 2 |
| 5 |
| 4 |
而AC为⊙O的直径,即半径为
| 3 |
| 2 |
∴点P到圆心O的距离小于圆的半径,
∴点P在⊙O内.
故选A.
点评:本题考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有点P在圆外?d>r;点P在圆上?d=r;点P在圆内?d<r.

练习册系列答案
相关题目
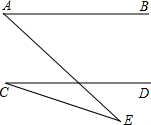 如图,AB∥CD,∠A=50°,∠C=24°,则∠E等于( )
如图,AB∥CD,∠A=50°,∠C=24°,则∠E等于( )| A、70° | B、26° |
| C、36° | D、16° |
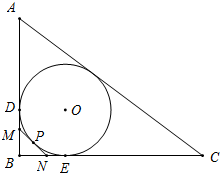 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=6cm,BC=8cm,则Rt△MBN的周长为