题目内容
不共线向量
,
的夹角为小于120°的角.且|
|=1,|
|=2,已知向量
=
+2
,求|
|的取值范围.
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| c |
. |
| a |
. |
| b |
. |
| c |
考点:*平面向量
专题:
分析:由不共线向量
,
的夹角为小于120°的角,求其余弦值的取值范围,然后求得|
|2的取值范围,继而求得答案.
| a |
. |
| b |
| c |
解答:解:设向量
,
的夹角为θ,则θ<120°,-
<cosθ≤1,
∵|
|2=
2=(
+2
)2=
2+4
•
+4
2=|
|2+4|
|×|
|cosθ+4|
|2=1+8cosθ+16=17+8cosθ,
∴13<|
|2≤25,
∴
<|
|≤5,
∴|
|的取值范围为:
<|
|≤5.
| a |
. |
| b |
| 1 |
| 2 |
∵|
| c |
| c |
. |
| a |
. |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
∴13<|
| c |
∴
| 13 |
| c |
∴|
. |
| c |
| 13 |
| c |
点评:此题考查了平面向量的知识.注意掌握数量模的概念是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
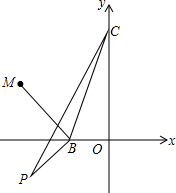 如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.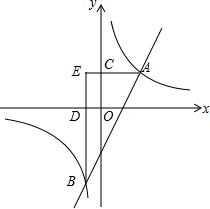 如图,双曲线y=
如图,双曲线y=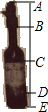 如图是一种盛装葡萄酒的瓶子,已知量得瓶塞AB与其下面部分BC的高度之比为2:3,C是BD的中点,且标签底部DE=
如图是一种盛装葡萄酒的瓶子,已知量得瓶塞AB与其下面部分BC的高度之比为2:3,C是BD的中点,且标签底部DE=