Question

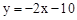 如图，直线与轴交于点A,直线交于点B,点C在线段AB上，⊙C与轴相切于点P，与OB切于点Q.

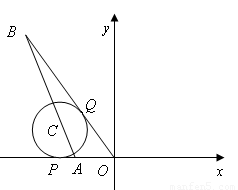
求：（1）A点的坐标;

（2）OB的长;

（3）C点的坐标.

 

Answer 1

【答案】

（1）（-5，0）；（2）（-8，6）；（3）（-6，2）．

【解析】

试题分析：（1）利用y=0，则-2x-10=0，进而求出x的值得出A点坐标即可；

（2）将直线与直线联立求出交点坐标即可；

（3）利用切线的性质以及三角形面积公式求出S_△BAO=S_△BCO+S_△AOC，进而得出C点纵坐标，即可得出答案．

试题解析：（1）∵直线与x轴交于点A，

∴y=0，则-2x-10=0，解得：x=-5.

∴A点的坐标为：（-5，0）.

（2）∵直线与x轴交于点A，直线交于点B，

∴,解得: .

∴B点坐标为:（-8，6）.

（3）如图,连接CQ，CP，

∵B点坐标为；（-8，6），∴可求得：BO=10.

∵点C在线段AB上，⊙C与x轴相切于点P，与OB切于点Q，∴CP⊥x轴，CQ⊥BO，PC=CQ.

∴S_△BAO=×6×5=S_△BCO+S_△AOC=（PC×5+CQ×BO）.

∴30=PC（5+10），解得：PC=2.

∴C点纵坐标为：2.

∴P点横坐标为：2=-2x-10，解得：x=-6.

∴C点坐标为：（-6，2）．

考点：1.直线上点的坐标与方程的关系;2. 三角形面积公式.