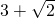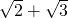题目内容
Given△ABC with∠ACB=90°，∠ABC=15°，AC=1，then the length of BC is（ ）
A、2+
| ||||
B、3+
| ||||
C、3-
| ||||
D、
|
分析：先作辅助线，作AD=BD，然后根据等腰三角形的知识，解出BD的长度，然后根据直角三角形的知识，再解出CD的长度，最后可得出BC的长．
解答：
解在BC上截取一点D，连接AD，使AD=BD
则∠DAB=∠DBA=15°
∴∠ADC=30°
又∵∠ACB=90°
∴AD=2AC
=2×1
=2
∵AD=BD
∴BD=2
∴CD=
=
=
∴BC=BD+CD
BC=2+
故选A
解在BC上截取一点D，连接AD，使AD=BD则∠DAB=∠DBA=15°
∴∠ADC=30°
又∵∠ACB=90°
∴AD=2AC
=2×1
=2
∵AD=BD
∴BD=2
∴CD=
| AD2-AC2 |
=
| 22-1 |
=
| 3 |
∴BC=BD+CD
BC=2+
| 3 |
故选A
点评：本题主要考查了等腰三角形的性质和解直角三角形的有关知识．在解题时要注意作辅助线，这是解题的关键．
练习册系列答案
相关题目
Given in the△ABC，a，b，c are three sides of the triangle，and
=
+
，then∠A is（ ）
（英汉词典acute angle：锐角；obtuse angle：钝角）
| 3 |
| a |
| 2 |
| b |
| 1 |
| c |
（英汉词典acute angle：锐角；obtuse angle：钝角）
| A、acute angle |
| B、right angle |
| C、obtues angle |
| D、acute angle or obtues angle |
Given in the △ABC ，a，b，c are three sides of the triangle，and
，then ∠A is
A．acute angle B．right angle
|