题目内容
如图,点A是反比例函数y= 的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=
的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=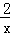 的图象于点C,则△OAC的面积为 .
的图象于点C,则△OAC的面积为 .

2 .
【考点】反比例函数系数k的几何意义.
【专题】代数几何综合题.
【分析】由于AB⊥x轴,根据反比例函数k的几何意义得到S△AOB=3,S△COB=1,然后利用S△AOC=S△AOB﹣S△COB进行计算.
【解答】解:∵AB⊥x轴,
∴S△AOB= ×|6|=3,S△COB=
×|6|=3,S△COB= ×|2|=1,
×|2|=1,
∴S△AOC=S△AOB﹣S△COB=2.
故答案为:2.
【点评】本题考查了反比例函数y= (k≠0)系数k的几何意义:从反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y= (k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
相关题目
 ×(﹣
×(﹣ )+|﹣2
)+|﹣2 |+(
|+(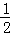 )﹣3.
)﹣3. B.
B. C.
C. D.
D.
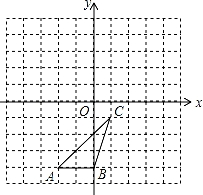
 ,则该三角形的周长为( )
,则该三角形的周长为( )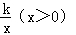 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.



 B.
B.
 C.3 D.2
C.3 D.2