题目内容
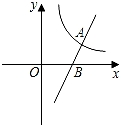
如图,直线y=2x﹣6与反比例函数y=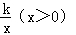 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

【考点】反比例函数综合题.
【专题】数形结合.
【分析】(1)先把(4,2)代入反比例函数解析式,易求k,再把y=0代入一次函数解析式可求B点坐标;
(2)假设存在,然后设C点坐标是(a,0),然后利用两点之间的公式可得 =
= ,借此无理方程,易得a=3或a=5,其中a=3和B点重合,舍去,故C点坐标可求.
,借此无理方程,易得a=3或a=5,其中a=3和B点重合,舍去,故C点坐标可求.
【解答】解:(1)把(4,2)代入反比例函数y=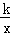 ,得
,得
k=8,
把y=0代入y=2x﹣6中,可得
x=3,
故k=8;B点坐标是(3,0);
(2)假设存在,设C点坐标是(a,0),
∵AB=AC,
∴ =
= ,
,
即(4﹣a)2+4=5,
解得a=5或a=3(此点与B重合,舍去)
故点C的坐标是(5,0).
【点评】本题考查了反比 函数的知识,解题的关键是理解点与函数的关系,并能灵活使用两点之间的距离公式.
函数的知识,解题的关键是理解点与函数的关系,并能灵活使用两点之间的距离公式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

 (x<0)分别交于点C、D,且C点的坐标为(﹣1,2).
(x<0)分别交于点C、D,且C点的坐标为(﹣1,2).

 的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=
的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=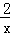 的图象于点C,则△OAC的面积为 .
的图象于点C,则△OAC的面积为 .



 B.﹣5 C.±5 D.﹣
B.﹣5 C.±5 D.﹣