题目内容
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点.若PB切⊙O于点B,则PB的最小值是( )


A.
 B.
B.
 C.3 D.2
C.3 D.2
B【考点】切线的性质.
【专题】计算题.
【分析】连结OB,如图,根据切线的性质得∠PBO=90°,则利用勾股定理有PB=
 =
=
 ,所以当点P运动到点P′的位置时,OP最小时,则PB最小,此时OP=3,然后计算此时的PB即可.
,所以当点P运动到点P′的位置时,OP最小时,则PB最小,此时OP=3,然后计算此时的PB即可.
【解答】解:连结OB,作OP′⊥l于P′如图,OP′=3,
∵PB切⊙O于点B,
∴OB⊥PB,
∴∠PBO=90°,
∴PB=
 =
=
 ,
,
当点P运动到点P′的位置时,OP最小时,则PB最小,此时OP=3,
∴PB的最小值为
 =
=
 .
.
故选B.


【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂线段最短.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.
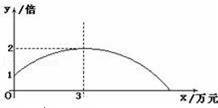
某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
| 成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
| 2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?

 的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=
的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=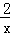 的图象于点C,则△OAC的面积为 .
的图象于点C,则△OAC的面积为 .





 B.
B.
 C.
C.
 D.
D.
