Question

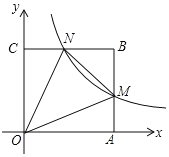
【题目】如图，在平面直角坐标系中，边长为1的正方形OABC的顶点O与原点重合，顶点A，C分别在x轴、y轴上，反比例函数y＝（k≠0，x＞0）的图象与正方形的两边AB、BC分别交于点M、N，连接OM、ON、MN．若∠MON＝45°，则k的值为_____．

Answer 1

【答案】﹣1

【解析】

由点M、N都在y=的图象上，及正方形的性质可得出 CN=AM，将△OAM绕点O逆时针旋转90°，可证出△M'ON≌△MON（SAS），由此即可得出M′N=MN，再由CN=AM，通过边与边之间的关系即可得出BM=BN，设AM=CN=x，则BM=BN=1-x，MN=2x，在Rt△BMN中，利用勾股定理列出x的方程，求得x的值，便可得出M点的坐标，最后用待定系数法求得k便可．

解：∵点M、N都在y＝的图象上，

∴S△ONC＝S△OAM＝|k|．

∵四边形ABCO为正方形，

∴OC＝OA，∠OCN＝∠OAM＝90°，

∴OCCN＝OAAM．

∴CN＝AM．

将△OAM绕点O逆时针旋转90°，点M对应M′，点A对应C，如图所示．

∵∠OCM′+∠OCN＝180°，

∴N、C、M′共线．

∵∠COA＝90°，∠NOM＝45°，

∴∠CON+∠MOA＝45°．

∵△OAM旋转得到△OCM′，

∴∠MOA＝∠M′OC，

∴∠CON+∠COM'＝45°，

∴∠M'ON＝∠MON＝45°．

在△M'ON与△MON中，

，

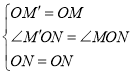∴△M'ON≌△MON（SAS），

∴MN＝M'N．

∵CN＝AM．

又∵BC＝BA，

∴BN＝BM．

设AM＝CN＝x，则BM＝BN＝1﹣x，MN＝2x，

又∵∠B＝90°，

∴BN2+BM2＝MN2，

∴(1﹣x)2+(1﹣x)2＝(2x)2，

解得，x＝﹣1，或x＝﹣﹣1（舍去），

∴AM＝﹣1，

∴M(1，﹣1)，

∵M点在反比例函数y＝（k≠0，x＞0）的图象上，

∴k＝1×(﹣1)＝﹣1，

故答案为：﹣1．