题目内容
4.已知?ABCD中,点E在AD上,AE=$\frac{1}{4}$AD,连接CE交BD于点F,则EF:FC的值是3:4.分析 证明△DEF∽△BCF后,可知$\frac{ED}{BC}=\frac{EF}{CF}$,根据AE=$\frac{1}{4}$AD即可求出答案.
解答  解:∵ED∥BC
解:∵ED∥BC
∴△DEF∽△BCF,
∴$\frac{ED}{BC}=\frac{EF}{CF}$,
∵AE=$\frac{1}{4}$AD,
∴$\frac{ED}{AD}=\frac{ED}{BC}$=$\frac{3}{4}$,
∴$\frac{EF}{BC}=\frac{3}{4}$
故答案为:3:4
点评 本题考查相似三角形的性质与判定,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.

练习册系列答案
相关题目
 (1)如图1,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD.
(1)如图1,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD. 如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12.
如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12.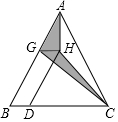 如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4.
如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4.