题目内容
3.已知直线y=kx+b(k≠0)过点(2,-3),(-2,m),且不经过第一象限,则m的取值范围是( )| A. | m<-2 | B. | m≤3 | C. | -2<m<3 | D. | -3<m≤3 |
分析 由直线不过第一象限即可得出k<0、b≤0,由点的坐标利用待定系数法即可求出k、b的值,进而即可得出关于m的一元一次不等式组,解之即可得出结论.
解答 解:∵直线y=kx+b(k≠0)不经过第一象限,
∴k<0,b≤0,
将(2,-3)、(-2,m)代入y=kx+b,
$\left\{\begin{array}{l}{2k+b=-3}\\{-2k+b=m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{3+m}{4}}\\{b=\frac{m-3}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{3+m>0}\\{m-3≤0}\end{array}\right.$,
解得:-3<m≤3.
故选D.
点评 本题考查了一次函数图象与系数的关系、待定系数法求一次函数解析式以及解一元一次不等式组,根据一次函数图象与系数的关系结合待定系数法求一次函数解析式找出关于m的一元一次不等式组是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.若一个三角形三个内角度数的比为1:2:3,那么这个三角形是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
 已知:如图,直线AB和CD相交于点O,射线OE⊥AB于点O,射线OF⊥CD于点O,且∠BOF=35°,求∠AOC和∠DOE的度数.
已知:如图,直线AB和CD相交于点O,射线OE⊥AB于点O,射线OF⊥CD于点O,且∠BOF=35°,求∠AOC和∠DOE的度数. 如图,已知△ABC.
如图,已知△ABC.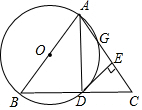 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作⊙O的切线DE,交AC于点E.求证: