题目内容
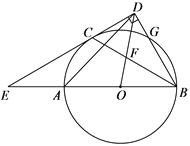
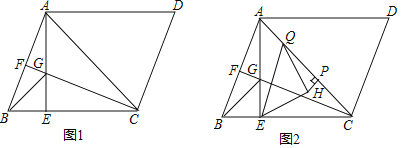
【题目】已知平行四边形
，过点
作
的垂线，垂足为点
，且满足
，过点
作
的垂线，垂足为点
，交
于点
，连接
．
（1）如图1，若
，
，求的长度；
（2）如图2取
上一点
，连接
，在
内取一点
，连接
，
，过点作的垂线，垂足为点
，若
，
．求证：
．
【答案】（1）
（2）证明见解析
【解析】
(1)根据已知条件可先求出
，再找到两个角一个边对应相等，证得
，求得BE，且BE=GE，利用勾股定理求得BG
(2) 作
交QH的延长线于M，连接CM，证明
（SAS），推出AQ=CM，再利用三角形的中位线定理解决问题即可.
（1）∵
，
，
∴
∵
∴
∵
∴
∵
∴
故答案：
（2）作交QH的延长线于M，连接CM
∵QH=EH， 
∴
∵
∴
∴
∴EQ=EM
∵
∴QH=HM
∵
∴
∵EA=EC，EQ=EM
∴
∴
∵
∴
∵
∴
∴HP∥CM
∴QP=PC
∵QH=HM
∴CM=2PH
∴AQ=2PH
练习册系列答案
相关题目
