题目内容
【题目】某水产品养殖企业为指导该企业某种产品的养殖和销售,对历年市场行情和水产品的养殖情况进行了调查.调查发现这种水产品的每千克售价![]() (元)与销售月份
(元)与销售月份![]() (月)满足关系式
(月)满足关系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)与销售月份
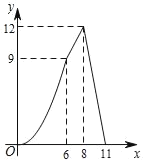
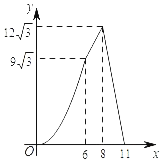
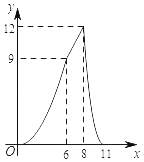
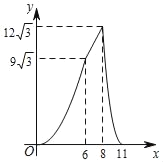
(元)与销售月份![]() (月)满足的函数关系如图所示:
(月)满足的函数关系如图所示:
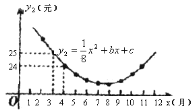
(1)试确定![]() 、
、![]() 的值;
的值;
(2)求出这种水产品每千克的利润![]() (元)与销售月份
(元)与销售月份![]() (月)之间的函数关系式;
(月)之间的函数关系式;
(3)几月份出售这种水产品每千克利润最大?最大利润是多少?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)6月份出售这种水产品每千克利润最大,最大利润是每千克11元.
;(3)6月份出售这种水产品每千克利润最大,最大利润是每千克11元.
【解析】
(1)把图中的已知坐标代入解析式,解方程组求出b,c即可;
(2)由题意得![]() ,化简函数关系式即可;
,化简函数关系式即可;
(3)已知y与x的函数关系式,用配方法化为顶点式,根据抛物线的性质即可求出最大值.
解:(1)根据图象,将![]() 和
和![]() 分别代入解析式
分别代入解析式![]() 得:
得:

解得:![]() ,
,![]() ;
;
(2)由题意得:![]() ,
,
∴![]()
(3)将![]() 化为顶点式得:
化为顶点式得:![]() ,
,
∵![]() ,
,
∴抛物线开口向下,
∴当![]() 时,二次函数取得最大值,此时y=11,
时,二次函数取得最大值,此时y=11,
所以6月份出售这种水产品每千克利润最大,最大利润是每千克11元。

 智慧小复习系列答案
智慧小复习系列答案【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有![]() 名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
[收集数据]
从甲、乙两校各随机抽取![]() 名学生,在这次竞赛中他们的成绩如下:
名学生,在这次竞赛中他们的成绩如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校 人数 成绩 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(说明:优秀成绩为![]() ,良好成绩为
,良好成绩为![]() 合格成绩为
合格成绩为![]() .)
.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校 | 平均分 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出结论]
(1)小明同学说:“这次竞赛我得了![]() 分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
(2)张老师从乙校随机抽取--名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为_ ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由: ;
(至少从两个不同的角度说明推断的合理性)