题目内容
14.某工厂投入生产一种机器,每台成本y(万元/台)与生产数量x(台)之间是一次函数关系,函数y与自变量x的部分对应值如下表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元/台) | 60 | 55 | 50 |
分析 设y与x的函数关系式为y=kx+b(k≠0),然后利用待定系数法求一次函数解析式解答.
解答 解:(1)设y与x的函数关系式为y=kx+b(k≠0),
则$\left\{\begin{array}{l}{10k+b=60}\\{20k+b=55}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=65}\end{array}\right.$,
因此y与x之间的函数关系式是y=-$\frac{1}{2}$x+65.
故答案为:y=-$\frac{1}{2}$x+65.
点评 此题考查根据实际问题列一次函数解析式,掌握待定系数法求函数解析式是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
2.分式方程x-$\frac{5}{x-2}$=2-$\frac{5}{x-2}$的解的情况是( )
| A. | 只有一解x=2 | B. | 任意实数都是解 | C. | 无解 | D. | 解为x≠2 |
9.甲队修路120m与乙队修路100m所用天数相同,已知甲队比乙队每天多修10m,设乙队每天修路xm.依题意,下面所列方程正确的是( )
| A. | $\frac{120}{x}=\frac{100}{x-10}$ | B. | $\frac{120}{x+10}=\frac{100}{x}$ | C. | $\frac{120}{x-10}=\frac{100}{x}$ | D. | $\frac{120}{x}=\frac{100}{x+10}$ |
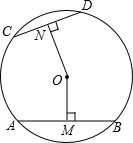 如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由.
如图所示,在⊙O中,AB,CD是两条弦,且AB>CD,OM⊥AB于点M,ON⊥CD于点N,请你猜想0M与0N的大小关系,并说明理由.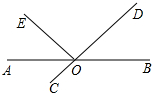 如图,直线AB,CD相交于点O,OA平分∠EOC.
如图,直线AB,CD相交于点O,OA平分∠EOC.