题目内容
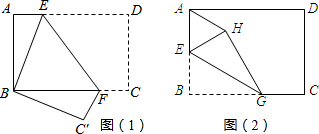
①如图1,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C’处,折痕为EF,若∠ABE=20°,那么∠EFC’的度数为
②如图2,已知矩形纸片ABCD,点E 是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为
125
125
°.②如图2,已知矩形纸片ABCD,点E 是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为
3
3
个
分析:(1)由折叠的性质知:∠EBC′、∠BC′F都是直角,因此BE∥C′F,那么∠EFC′和∠BEF互补,欲求∠EFC′的度数,需先求出∠BEF的度数;根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,由此可求出∠BEF的度数,即可得解.
(2)根据折叠的性质可得∠BEG=∠HEG,BE=EH,从而得出∠EAH=∠EHA,根据∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,可得∠BEG=∠EAH,继而可得出答案.
(2)根据折叠的性质可得∠BEG=∠HEG,BE=EH,从而得出∠EAH=∠EHA,根据∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,可得∠BEG=∠EAH,继而可得出答案.
解答:解:(1)Rt△ABE中,∠ABE=20°,
∴∠AEB=70°;
由折叠的性质知:∠BEF=∠DEF;
而∠BED=180°-∠AEB=110°,∴∠BEF=55°;
∵∠EBC′=∠D=∠BC′F=∠C=90°,
∴BE∥C′F,
∴∠EFC′=180°-∠BEF=125°.
故答案为:125;
(2)由折叠的性质得,∠BEG=∠HEG,BE=EH,
故可得∠EAH=∠EHA(等腰三角形的性质),
∵∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,
∴∠BEG=∠HEG=∠EAH=∠EHA,
故与∠BEG相等的角的个数为3个.
故答案为:3.
∴∠AEB=70°;
由折叠的性质知:∠BEF=∠DEF;
而∠BED=180°-∠AEB=110°,∴∠BEF=55°;
∵∠EBC′=∠D=∠BC′F=∠C=90°,
∴BE∥C′F,
∴∠EFC′=180°-∠BEF=125°.
故答案为:125;
(2)由折叠的性质得,∠BEG=∠HEG,BE=EH,
故可得∠EAH=∠EHA(等腰三角形的性质),
∵∠AEH+∠EAH+∠EHA=180°,∠AEH+∠EHG+∠BEG=180°,
∴∠BEG=∠HEG=∠EAH=∠EHA,
故与∠BEG相等的角的个数为3个.
故答案为:3.
点评:此题考查了折叠的性质,根据题意得出∠BEG=∠HEG,BE=EH,利用等腰三角形的性质解答是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 ,
, 重合),压平后得到折痕
重合),压平后得到折痕 .
.
 时,求
时,求 的值.(方法指导:为了求得
的值.(方法指导:为了求得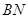 、
、 的长,不妨设
的长,不妨设 =2)
=2) 则
则 则
则 (
( 为整数),则
为整数),则 重合),压平后得到折痕
重合),压平后得到折痕 设
设 则
则 的式子表示)
的式子表示)