题目内容
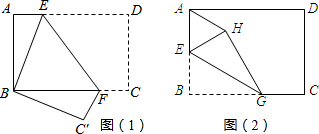
18、如图2,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AEF的度数为

67.5°
.
分析:根据翻折前后角度不发生变化,第一次折叠求出∠EAD的度数,再利用第2次翻折,得出∠AFE=∠EFA′以及度数,从而求出∠AEF的度数.
解答: 解:根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,
解:根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,
∴∠EAD=45°,
∵过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,
∴∠EA′F=∠FAE=45°,
∴∠AFE=∠EFA′=(180°-45°)÷2=67.5°,
∴∠AEF=∠FEA′=180°-67.5°-45°=67.5°.
故答案为:67.5°.
 解:根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,
解:根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,∴∠EAD=45°,
∵过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,
∴∠EA′F=∠FAE=45°,
∴∠AFE=∠EFA′=(180°-45°)÷2=67.5°,
∴∠AEF=∠FEA′=180°-67.5°-45°=67.5°.
故答案为:67.5°.
点评:此题主要考查了翻折变换,利用翻折变换前后角不发生大小变化是解决问题的关键.

练习册系列答案
相关题目


 折叠,使点
折叠,使点 落在
落在 边上一点
边上一点 (不与点
(不与点 ,
, 重合),压平后得到折痕
重合),压平后得到折痕 .
.
 时,求
时,求 的值.(方法指导:为了求得
的值.(方法指导:为了求得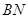 、
、 的长,不妨设
的长,不妨设 =2)
=2) 则
则 则
则 (
( 为整数),则
为整数),则 重合),压平后得到折痕
重合),压平后得到折痕 设
设 则
则 的式子表示)
的式子表示)