题目内容
7. 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=20°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=20°,求∠FEC的度数.
分析 根据平行于同一条直线的两直线平行可得EF∥BC,再根据平行线的性质可得∠ACB+∠DAC=180°,进而可得∠ACB的度数,然后求出∠FCB的度数,再根据角平分线的性质可得∠BCE=22°.再利用平行线的性质可得答案.
解答 解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∵AD∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=116°,
∴∠ACB=64°,
∵∠ACF=20°,
∴∠FCB=∠ACB-∠ACF=44°,
∵CE平分∠BCF,
∴∠BCE=22°.
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=22°.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同位角相等,内错角相等,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次活动汇总后统计的数据:
(1)请估计:当次数S很大时,摸到白球的频率将会接近0.3;假如你去摸一次,你摸到红球的概率是0.7(精确到0.1).
(2)试估算口袋中红球有多少只?
| 摸球的次数S | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率 | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
18.下列计算结果,正确的是( )
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{3}$×$\sqrt{4}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | (-$\sqrt{3}$)2=-3 |
19. 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
 如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )
如图,数轴上,AB=AC,A,B两点对应的实数分别是$\sqrt{3}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
17.三元一次方程组$\left\{\begin{array}{l}{x+y=1}\\{y+z=5}\\{z+x=6}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\\{z=0}\end{array}\right.$ |
 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.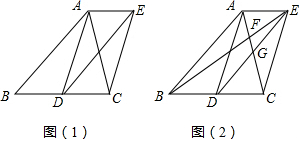
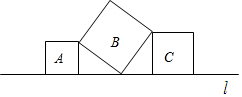 如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.
如图,直线l上有三个正方形A,B,C,若正方形A,C的面积分别为6,8,则正方形B的面积为14.