题目内容
.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
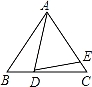
A.9 B.12 C.15 D.18
A【考点】相似三角形的判定与性质;等边三角形的性质.
【专题】压轴题.
【分析】由∠ADE=60°,可证得△ABD∽△DCE;可用等边三角形的边长表示出DC的长,进而根据相似三角形的对应边成比例,求得△ABC的边长.
【解答】解:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC;
∴CD=BC﹣BD=AB﹣3;
∴∠BAD+∠ADB=120°
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE;
∴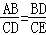 ,
,
即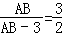 ;
;
解得AB=9.
故选:A.
【点评】此题主要考查了等边三角形的性质和相似三角形的判定和性质,能够证得△ABD∽△DCE是解答此题的关键.

练习册系列答案
相关题目
 中,
中, 若
若 ,则
,则 的度数是( ).
的度数是( ). B.
B. C.
C. D.
D.

 中,
中, 为
为 中点,
中点, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 .求证:(1)
.求证:(1) ≌
≌ ;(2)
;(2) .
.
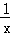 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( ) 上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是 .
上,AB⊥x轴于点B,且△AOB的面积是2,则k的值是 .
 、
、 为两个连续的整数,且
为两个连续的整数,且 ,则
,则 .
.