题目内容
已知⊙O的直径AB垂直于弦CD,垂足为E,若⊙O的半径是3米,且OE=EB,则劣弧
的长是( )
 |
| CD |
| A、π米 | ||
| B、2π米 | ||
C、
| ||
D、
|
分析:根据OE=EB=
OD,可将∠BOD的角求出,进而可将圆心角∠COD的角度求出,根据扇形的弧长公式可将
求出.
| 1 |
| 2 |
 |
| CD |
解答:解:∵OE=EB=
OD,
∴∠BOD=60°,
∵直径AB垂直于弦CD,
∴CE=DE,
∵∠OEC=∠OED,OE=OE,
∴△OEC≌△OED,
∴∠COD=2∠BOD=120°,
=
π×3=2π,
即劣弧
的长为2π.
故选B.
| 1 |
| 2 |
∴∠BOD=60°,
∵直径AB垂直于弦CD,
∴CE=DE,
∵∠OEC=∠OED,OE=OE,
∴△OEC≌△OED,
∴∠COD=2∠BOD=120°,
 |
| CD |
| 120 |
| 180 |
即劣弧
 |
| CD |
故选B.
点评:本题主要是应用垂径定理和特殊的三角函数值将圆心角求出,从而将劣弧的长求出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知⊙O的直径AB垂直于弦CD,垂足为G,F是CD延长线上的一点,AF交⊙O于点E,连接CE.若CF=10,
如图,已知⊙O的直径AB垂直于弦CD,垂足为G,F是CD延长线上的一点,AF交⊙O于点E,连接CE.若CF=10,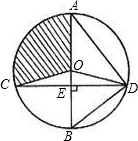 如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5. (2012•亭湖区一模)如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G.
(2012•亭湖区一模)如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G. 如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.