题目内容
 (2012•亭湖区一模)如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G.
(2012•亭湖区一模)如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G.求证:AC2=AG•AF.
分析:连接CG,由⊙O的直径AB垂直于弦CD,根据垂径定理得弧AD=弧AC,则∠ADC=∠ACF,根据圆周角定理得∠AGC=∠ADC,于是有∠ACF=∠AGC 根据相似三角形的判定易得△ACG∽△AFC,
=
,即可得到结论.
| AC |
| AG |
| AF |
| AC |
解答:证明:连接AD、CG,如图
∵直径AB⊥CD,
∴弧AD=弧AC,
∴∠ADC=∠ACF,
∵∠AGC=∠ADC,
∴∠ACF=∠AGC
而∠FAC=∠CAG,
∴△ACG∽△AFC,
∴
=
,
∴AC2=AG•AF.

∵直径AB⊥CD,
∴弧AD=弧AC,
∴∠ADC=∠ACF,
∵∠AGC=∠ADC,
∴∠ACF=∠AGC
而∠FAC=∠CAG,
∴△ACG∽△AFC,
∴
| AC |
| AG |
| AF |
| AC |
∴AC2=AG•AF.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了圆周角定理和三角形相似的判定与性质.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 (2012•亭湖区一模)如图,是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1,A2,A3,….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,…,依此类推.则第20圈的长为
(2012•亭湖区一模)如图,是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1,A2,A3,….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,…,依此类推.则第20圈的长为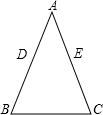 (2012•亭湖区一模)如图,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论.
(2012•亭湖区一模)如图,△ABC中,AB=AC,若点D在AB上,点E在AC上,请你加上一个条件,使结论BE=CD成立,同时补全图形,并证明此结论.