Question

19．课本P152有段文字：把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度，就得到函数y=2x+3或y=2x-3的图象．
【阅读理解】
小尧阅读这段文字后有个疑问：把函数y=-2x的图象沿x轴向右平移3个单位长度，如何求平移后的函数表达式？
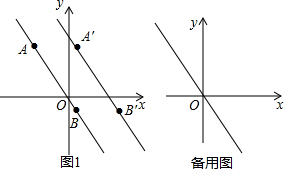
老师给了以下提示：如图1，在函数y=-2x的图象上任意取两个点A、B，分别向右平移3个单位长度，得到A′、B′，直线A′B′就是函数y=-2x的图象沿x轴向右平移3个单位长度后得到的图象．
请你帮助小尧解决他的困难．
（1）将函数y=-2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为C．
A．y=-2x+3；B．y=-2x-3；C．y=-2x+6；D．y=-2x-6
【解决问题】
（2）已知一次函数的图象与直线y=-2x关于x轴对称，求此一次函数的表达式．
【拓展探究】
（3）一次函数y=-2x的图象绕点（2，3）逆时针方向旋转90°后得到的图象对应的函数表达式为y=$\frac{1}{2}$x-$\frac{3}{2}$．（直接写结果）

Answer 1

分析 （1）平移时k的值不变，只有b发生变化．
（2）直接根据平面直角坐标系中，点关于x轴对称的特点得出答案；
（3）直接根据一次函数互相垂直时系数之积为-1，进而得出答案．

解答 解：（1）将函数y=-2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为y=-2x+6，
故选C；
（2）在函数y=-2x的图象上取两个点A（0，0）、B（1，-2），
关于x轴对称的点的坐标A′（0，0）、B′（1，2），
一次函数的表达式为y=2x；
（3）∵一次函数y=-2x的图象绕点（2，3）逆时针方向旋转90°，
∴旋转后得到的图象与原图象垂直，则对应的函数解析式为：y=$\frac{1}{2}$x-$\frac{3}{2}$．
故答案为：y=$\frac{1}{2}$x-$\frac{3}{2}$．

点评 本题考查图形的平移变换和函数解析式之间的关系．在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．平移后解析式有这样一个规律“左加右减，上加下减”．关键是要搞清楚平移前后的解析式有什么关系．