题目内容
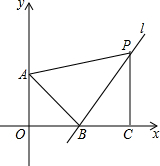 如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别是(0,3)(4,0),作直线l垂直AB,点P是直线l上的一个动点,作PC垂直x轴,垂足为C,连接AP,设点P的横坐标为a,在x轴上取点Q,使得以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标.
如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别是(0,3)(4,0),作直线l垂直AB,点P是直线l上的一个动点,作PC垂直x轴,垂足为C,连接AP,设点P的横坐标为a,在x轴上取点Q,使得以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标.考点:平行四边形的判定,坐标与图形性质
专题:
分析:根据已知求出OA=3,OB=4,AB=5,画出符合条件的两个图形,①当P在x轴的上方时,证△AOB∽△PBA,得出比例式,求出AP即可;②当p在x轴的下方时,过P作PM⊥x轴于M,证△AOQ∽△BOA,得出比例式,求出AQ=
,即BP=AQ=
,证△AOB∽△BMP,得出比例式,求出PM和BM,即可得出答案.
| 15 |
| 4 |
| 15 |
| 4 |
解答:解:∵点A,B的坐标分别是(0,3)(4,0),
∴OA=3,OB=4,由勾股定理得:AB=5,
分为两种情况:①当P在x轴的上方时,如图1,

∵A、P、B、Q组成的四边形是平行四边形,
∴P点的纵坐标和A点的纵坐标相同,都是3,且AP∥x轴,
∴∠PAB=∠ABO,
∵∠ABP=∠AOB=90°,
∴△AOB∽△PBA,
∴
=
,
∴
=
,
∴AP=
,
即P的坐标为(
,3);
②当p在x轴的下方时,如图2,过P作PM⊥x轴于M,

则∠AOB=∠PMB=∠ABP=90°,
∵∠ABP=90°,四边形ABPQ是平行四边形,
∴AQ=BP,∠QAB=90°,
∴∠AQO+∠QAO=90°,∠QAO+∠BAO=90°,
∴∠AQO=∠BAO,
∴△AOQ∽△BOA,
∴
=
,
∴
=
,
∴AQ=
,
即BP=AQ=
,
∵∠OAB+∠ABO=90°,∠ABO+∠PBM=90°,
∴∠OAB=∠PBM,
∴△AOB∽△BMP,
∴
=
=
,
∴
=
=
.
∴BM=
,PM=3,
∴OM=4-
=
,
即P的坐标为(
,-3).
∴OA=3,OB=4,由勾股定理得:AB=5,
分为两种情况:①当P在x轴的上方时,如图1,

∵A、P、B、Q组成的四边形是平行四边形,
∴P点的纵坐标和A点的纵坐标相同,都是3,且AP∥x轴,
∴∠PAB=∠ABO,
∵∠ABP=∠AOB=90°,
∴△AOB∽△PBA,
∴
| AB |
| OB |
| AP |
| AB |
∴
| 5 |
| 4 |
| AP |
| 5 |
∴AP=
| 25 |
| 4 |
即P的坐标为(
| 25 |
| 4 |
②当p在x轴的下方时,如图2,过P作PM⊥x轴于M,

则∠AOB=∠PMB=∠ABP=90°,
∵∠ABP=90°,四边形ABPQ是平行四边形,
∴AQ=BP,∠QAB=90°,
∴∠AQO+∠QAO=90°,∠QAO+∠BAO=90°,
∴∠AQO=∠BAO,
∴△AOQ∽△BOA,
∴
| AQ |
| AB |
| AO |
| OB |
∴
| AQ |
| 5 |
| 3 |
| 4 |
∴AQ=
| 15 |
| 4 |
即BP=AQ=
| 15 |
| 4 |
∵∠OAB+∠ABO=90°,∠ABO+∠PBM=90°,
∴∠OAB=∠PBM,
∴△AOB∽△BMP,
∴
| AB |
| BP |
| OA |
| BM |
| OB |
| PM |
∴
| 5 | ||
|
| 3 |
| BM |
| 4 |
| PM |
∴BM=
| 9 |
| 4 |
∴OM=4-
| 9 |
| 4 |
| 7 |
| 4 |
即P的坐标为(
| 7 |
| 4 |
点评:本题考查了平行四边形的性质,相似三角形的性质和判定,三角形内角和定理,坐标与图形性质的应用,能综合运用性质进行推理和计算是解此题的关键,用了分类讨论思想,有一定的难度.

练习册系列答案
相关题目
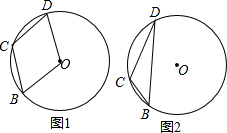 已知D、B、C是⊙O上三点
已知D、B、C是⊙O上三点
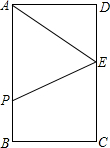 如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方向在矩形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.
如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方向在矩形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts. 如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.
如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.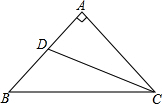 如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,AD=1,求△ABC的周长与面积.
如图,在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,AD=1,求△ABC的周长与面积.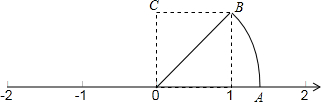 如图,四边形OEBC为正方形.
如图,四边形OEBC为正方形.