ƒøƒ⁄»ð
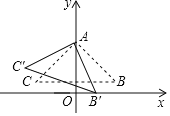
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþC1£∫y=ax2+bx-1æ≠π˝µ„A£®-2£¨1£©∫Õµ„B£®-1£¨-1£©£¨≈◊ŒÔœþC2£∫y=2x2+x+1£¨∂Ø÷±œþx=t”Î≈◊ŒÔœþC1Ωª”⁄µ„N£¨”Î≈◊ŒÔœþC2Ωª”⁄µ„M£Æ
£®1£©«Û≈◊ŒÔœþC1µƒ±Ì¥Ô Ω£ª
£®2£©÷±Ω””√∫¨tµƒ¥˙ ˝ Ω±Ì æœþ∂ŒMNµƒ≥§£ª
£®3£©µ±°˜AMN «“‘MNŒ™÷±Ω«±þµƒµ»—¸÷±Ω«»˝Ω«–Œ ±£¨«Ûtµƒ÷µ£ª
£®4£©‘⁄£®3£©µƒÃıº˛œ¬£¨…Ë≈◊ŒÔœþC1”Îy÷·Ωª”⁄µ„P£¨µ„M‘⁄y÷·”“≤ýµƒ≈◊ŒÔœþC2…œ£¨¡¨Ω”AMΩªy÷·”⁄µ„K£¨¡¨Ω”KN£¨‘⁄∆Ω√ʃ⁄”–“ªµ„Q£¨¡¨Ω”KQ∫ÕQN£¨µ±KQ=1«“°œKNQ=°œBNP ±£¨«Î÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£Æ

°æ¥∞∏°ø£®1£©y£Ωx2£´x£≠1£ª£®2£©t2+2£ª£®3£©1ªÚ0£ª£®4£©Qµ„◊¯±ÍŒ™£∫£®0£¨2£©°¢£®-1£¨3£©°¢![]() .
.
°æΩ‚Œˆ°ø
£®1£©”¶”√¥˝∂®œµ ˝∑®£ª
£®2£©∞—x=t¥¯»Î∫Ø ˝πÿœµ Ωœýºı£ª
£®3£©∏˘æðÕº–Œ∑÷±Ã÷¬€°œANM=90°„°¢°œAMN=90°„ ±µƒ«Èøˆ£Æ
£®4£©∏˘æ𓂪≠≥ˆ¬˙◊„Ãıº˛Õº–Œ£¨ø…“‘’“µΩANŒ™°˜KNP∂‘≥∆÷·£¨”…∂‘≥∆–‘’“µΩµ⁄“ª∏ˆ¬˙◊„Ãıº˛Q£¨‘ŸÕ®π˝—”≥§∫Õ‘≤µƒ∂‘≥∆–‘’“µΩ £”ý»˝∏ˆµ„£Æ¿˚”√π¥π…∂®¿ÌΩ¯––º∆À„£Æ
£®1£©°þ≈◊≈◊ŒÔœþC1£∫y£Ωax2£´bx£≠1æ≠π˝µ„A£®£≠2£¨1£©∫Õµ„B£®£≠1£¨£≠1£©£¨
°ý![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
°ý≈◊≈◊ŒÔœþC1µƒΩ‚Œˆ ΩŒ™y£Ωx2£´x£≠1£ª
£®2£©°þ∂Ø÷±œþx=t”Î≈◊ŒÔœþC1Ωª”⁄µ„N£¨”Î≈◊ŒÔœþC2Ωª”⁄µ„M
°ýµ„Nµƒ◊ð◊¯±ÍŒ™t2+t-1£¨µ„Mµƒ◊ð◊¯±ÍŒ™2t2+t+1
°ýMN=£®2t2+t+1£©-£®t2+t-1£©=t2+2
£®3£©π≤∑÷¡Ω÷÷«Èøˆ
¢Ÿµ±°œANM=90°„£¨AN=MN ±£¨”…“—÷™N£®t£¨t2+t-1£©£¨A£®-2£¨1£©
°ýAN=t-£®-2£©=t+2
°þMN=t2+2
°ýt2+2=t+2
°ýt1=0£®…·»•£©£¨t2=1
°ýt=1
¢⁄µ±°œAMN=90°„£¨AM=MN ±£¨”…“—÷™M£®t£¨2t2+t+1£©£¨A£®-2£¨1£©
°ýAM=t-£®-2£©=t+2£¨
°þMN=t2+2
°ýt2+2=t+2
°ýt1=0£¨t2=1£®…·»•£©
°ýt=0
π tµƒ÷µŒ™1ªÚ0
£®4£©”…£®3£©ø…÷™t=1 ±MŒª”⁄y÷·”“≤ý£¨∏˘æ𓂪≠≥ˆ æ“‚Õº»ÁÕº£∫

“◊µ√K£®0£¨3£©£¨B°¢O°¢N»˝µ„π≤œþ
°þA£®-2£¨1£©N£®1£¨1£©P£®0£¨-1£©
°ýµ„K°¢Pπÿ”⁄÷±œþAN∂‘≥∆
…Ë∞Îæ∂Œ™1µƒ°—K”Îy÷·œ¬∑ΩΩªµ„Œ™Q2£¨‘Ú∆‰◊¯±ÍŒ™£®0£¨2£©
°ýQ2”ε„Oπÿ”⁄÷±œþAN∂‘≥∆
°ýQ2 «¬˙◊„Ãıº˛°œKNQ=°œBNP£Æ
‘ÚNQ2—”≥§œþ”ΰ—KΩªµ„Q1£¨Q1°¢Q2πÿ”⁄KNµƒ∂‘≥∆µ„Q3°¢Q4“≤¬˙◊„°œKNQ=°œBNP£Æ
”…Õº–Œ“◊µ√Q1£®-1£¨3£©
…˵„Q3◊¯±ÍŒ™£®m£¨n£©£¨”…∂‘≥∆–‘ø…÷™Q3N=NQ1=BN=2![]()
”…°þ°—K∞Îæ∂Œ™1
°ý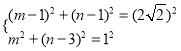
Ω‚µ√ £¨£Æ
£¨£Æ
Õ¨¿Ì£¨…˵„Q4◊¯±ÍŒ™£®m£¨n£©£¨”…∂‘≥∆–‘ø…÷™Q4N=NQ2=NO=![]()
°ý
Ω‚µ√ £Æ
£Æ
°ý¬˙◊„Ãıº˛µƒQµ„◊¯±ÍŒ™£∫£®0£¨2£©°¢£®-1£¨3£©°¢![]()

 º∆À„∏þ ÷œµ¡–¥∞∏
º∆À„∏þ ÷œµ¡–¥∞∏°æƒø°øƒ≥≥¨ –œ˙ €“ª÷÷…Ã∆∑£¨≥…±æ√ø«ßøÀ40‘™£¨πÊ∂®√ø«ßøÀ €º€≤ªµÕ”⁄≥…±æ£¨«“≤ª∏þ”⁄80‘™£¨æ≠ –≥°µ˜≤È£¨√øÃϵƒœ˙ €¡øy£®«ßøÀ£©”Î√ø«ßøÀ €º€x£®‘™£©¬˙◊„“ª¥Œ∫Ø ˝πÿœµ£¨≤ø∑÷ ˝æð»Áœ¬±Ì£∫
€º€x£®‘™/«ßøÀ£© | 50 | 60 | 70 |
œ˙ €¡øy£®«ßøÀ£© | 100 | 80 | 60 |
£®1£©«Ûy”Îx÷ƺ‰µƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©…Ë…Ã∆∑√øÃϵƒ◊п˚»ÛŒ™W£®‘™£©£¨‘Úµ± €º€x∂®Œ™∂ý…Ÿ‘™ ±£¨≥ß…Ã√øÃσЪҵ√◊Ó¥Û¿˚»Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
£®3£©»Áπ˚≥¨ –“™ªÒµ√√øÃÏ≤ªµÕ”⁄1350‘™µƒ¿˚»Û£¨«“∑˚∫œ≥¨ –◊‘º∫µƒπÊ∂®£¨ƒ«√¥∏√…Ã∆∑√ø«ßøÀ €º€µƒ»°÷µ∑∂Œß «∂ý…Ÿ£ø«ÎÀµ√˜¿Ì”…£Æ