题目内容
已知在Rt△ABC中，∠C=90°，cosB=
，则tanA的值为
- A.2
- B.
- C.
- D.
D
分析：首先根据锐角三角函数的定义，结合勾股定理，用同一个未知数表示直角三角形的三边；再根据锐角三角函数的定义求解．
解答：由cosB=，可设a=x，c=2x，由勾股定理得：b=
=x，
∴tanA=
=
=，
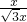故选：D．
点评：此题考查的知识点是互余两角三角函数的关系，求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值．
分析：首先根据锐角三角函数的定义，结合勾股定理，用同一个未知数表示直角三角形的三边；再根据锐角三角函数的定义求解．
解答：由cosB=
，可设a=x，c=2x，由勾股定理得：b==x，∴tanA=
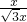==，故选：D．
点评：此题考查的知识点是互余两角三角函数的关系，求锐角的三角函数值的方法：利用锐角三角函数的定义，通过设参数的方法求三角函数值，或者利用同角（或余角）的三角函数关系式求三角函数值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2的值等于（ ）
（1）已知在Rt△ABC中，∠C=90°，sinA=